Optimization of Heating Parameters for Hot Forming Operation

Test Case Description

In this example a two-stage processing of an axisymmetric billet with length L=30 mm and radius r=10 mm is considered:

Heating: In the first stage the billet at initial temperature 20° C is heated at x=L with a heat flux F_o for time t_h while the surface at x=0 is kept at initial temperature. Other surfaces are isolated.
Forming: In the second stage the billet is deformed in such a way that prescribed displacement at x=L is u_x=-2 mm and at x=0 is u_x=0. Other surfaces are free. The deformation is modeled by an ideal elasto-plastic material model where flow stress depends on temperature. No heat transfer is assumed in the second stage. Material properties are summarized in Tables 1 and 2.

The discretized configurations of the specimen before and after heating and forming are illustrated in Figure 1 and 2, respectively. Only half of the domain is represented due to the symmetry condition.

Figure 1: Temperature distribution after heating. The heat flux
F_o=3.500 W/m² is applied for t_h=10 s.

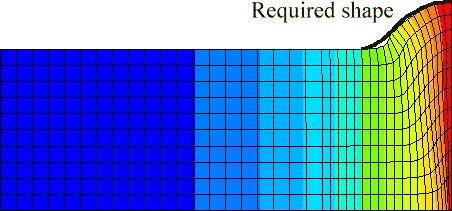Figure 2: Effective stress distribution in the deformed specimen after forming. The heat flux
F_o=3.500 W/m² is applied for t_h=10 s. Displacement of the right surface u_x=-2 mm.

Table 1: Material properties

Thermal conductivity (K)	30	[W/mK]
Heat capacity (C)	500	[J/kg K]
Density (r)	7850	[kg/m³]
Youngs module (E)	210000	[MPa]
Poissons ratio (n)	0.3	[/]

Table 2: Yield stress as a function of temperature

Temperature [^oC]	Yield stress [MPa]
20	700
100	620
200	560
300	540
400	510
500	500
600	390
700	200
800	180
900	150
1000	120
1100	90
1200	60

Definition of the Optimization Problem

Find optimal heating parameters defined by heat flux F_o and heating time t_h so that the difference between required and computed shapes of the specimen after forming is minimum. The objective function to be minimised is expressed in terms of differences of the required and computed node coordinates in the interval 20mm £ x £ 28mm. The choice of heating parameters is constrained by maximum permissible temperature of the specimen T_max=1200^oC. The constraint is presented in Figure 3.

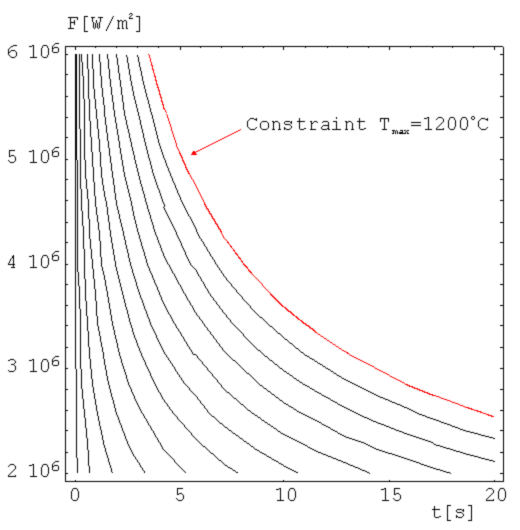
Figure 3: Constraint imposed on the choice of heating parameters. Contours show maximum temperature of the specimen as a function of applied heat flux and heating time. Spacing between contours is 100^oC

We introduce the constrain to the objective function by adding the temperature term, which increases rapidly when the maximum temperature of the billet is coming near to the permissible temperature. The objective function for this case is:

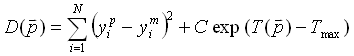(1)

The parameter vector (F, t_h) is denoted by . Prescribed node coordinates are denoted by upper index p and the measured node coordinates are denoted by upper index m. Maximum temperature at the right end of the billet after the heating is denoted by .

Heat flux and heating time can only have positive values. To assure that during the optimization algorithm a transformation function that maps the parameters from [-¥,¥] to [0,¥] must be applied.

(2)

(3)

The billet deformation after the forming depends on the billet temperature distribution that can be calculated by the following equation:

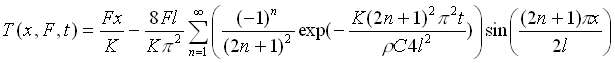(4)

Temperature distributions for three different heating regimes are presented in figure 4.

Figure 4: Temperature distributions along x-axis for three different heating regimes

Different temperature distributions result in different shapes of the billet after the forming. Shapes for the temperature distributions from the figure 4 are presented in figure 5.

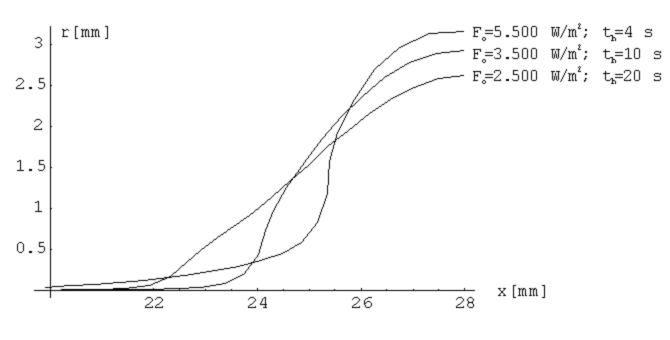
Figure 5: Deformed shapes of the specimen after forming for three different heating regimes

The required shape of the billet after both stages of forming is prescribed by the following sigmoidal function:

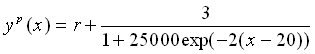(5)

Results

The optimization was done by the inverse shell using the nonlinear simplex method. Optimal solution was found in 34 iterations. The required shape and shape at the optimal parameters is presented in figure 6.

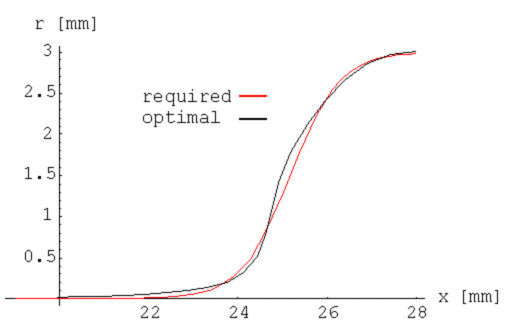
Figure 6: Required and optimal shape of the billet at the optimal solution
F_opt= 3628674.9 W/m², t_opt= 7.99 s, D(_opt) = 0.1448.

The shell also includes functions for tabelating. Since the case only has two parameters it is possible to plot the objective function in the finite domain of the parameter space. Figure 7 shows 19x17 points diagram of the objective function. The temperature constrain term is ommited.

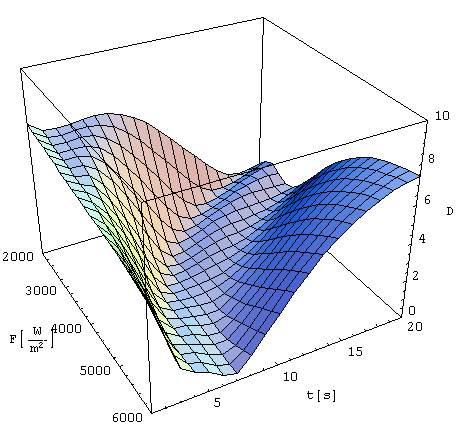
Figure 7: Objective function on the finite domain of the parameter space (19x17 points). The temperature constrain term is omitted.

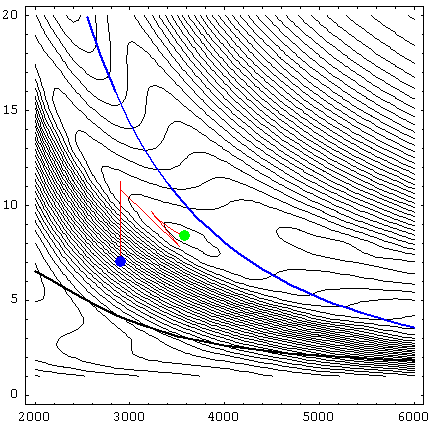
Figure 8: Conture of the objective function with maximal temperature constraint (blue), maximal force constraint (black) and optimal solution (red path starting in blue point and ending in green point) included.