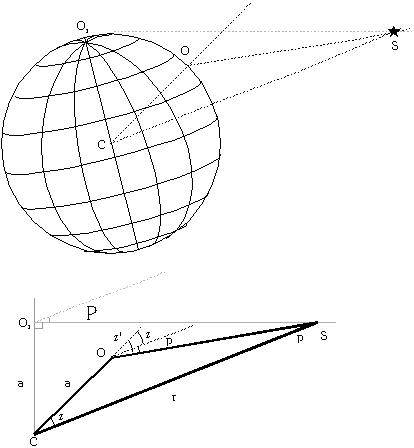
Our observations are made from the surface of the Earth, not its centre. This is irrelevant when observing distant objects such as stars. But for closer objects (e.g. within the Solar System), a correction must be made.

To an observer at O, the zenith angle of object S appears to be z'. Its true zenith angle, as seen from the centre of the Earth C, is z.
Refraction decreases zenith angle, but parallax increases it.
Define the angle of parallax p by p = z'-z.
If a is the Earth's radius, and r is the
geocentric distance to object, then the plane triangle OCS gives:
sin(p) / a = sin(180°-z') / r = sin(z')
/ r
that is,
sin(p) = a / r sin(z')
Parallax is greatest for an observer at O1,
where the object appears to be on the horizon. The horizontal parallax
P = 90°-z, where
sin(P) = a / r.
So in the general case, we may write
sin(p) = sin(P) sin(z')
or, since angles of parallax are small,
p = P sin(z')

The Moon is the nearest natural object, with average P
around 57 arc-minutes.
For calculating times of moonrise and moonset, we must use an altitude
of
0° - 16' [semi-diameter] - 34' [refraction] + 57' [horizontal parallax]
= +7'.

Allowing for lunar parallax is essential when predicting
occultations of stars by the Moon
(and, of course, solar eclipses).

The Earth is not actually spherical.
For more accurate calculations, use a spheroidal solid
which approximates Earth's true shape (the geoid).
For any particular latitude, this gives corrected values for geocentric
distance a and geocentric latitude.
Return to index.