Positional Astronomy:
Refraction

The apparent position of an object in the sky may be changed by several different physical effects. One of these is refraction.

The speed of light changes as it passes through a medium such as air. Define the refractive index of any transparent medium as 1/(the speed of light in that medium).

The speed of light in air depends on its temperature and its pressure, so the refractive index of the air varies in different parts of the atmosphere.

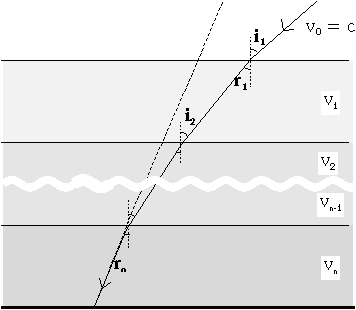
Make a simple model of the atmosphere as n layers of uniform air above a flat Earth, with a different velocity of light vi for each layer (i from 1 to n). Apply Snell's Law of Refraction at each boundary.

At the first boundary, sin(i1)/sin(r1) = v0/v1.
At the next boundary, sin(i2)/sin(r2) = v1/v2, and so on.
But, by simple geometry, r1 = i2, r2 = i3 and so on.
So we have
sin(i1) = (v0/v1) sin(r1)
          = (v0/v1) sin(i2)
          = (v0/v1) (v1/v2) sin(r2)
          = (v0/v2) sin(r2)
          = ..........
          = (v0/vn) sin(rn)

The refractive indices of the intervening layers all cancel out. The only thing that matters is the ratio between v0 (which is c, the speed of light in vacuum) and vn (the speed in the air at ground level).

rn is the apparent zenith distance of the star, z', and i1 is its true zenith distance, z.
Refraction has no effect if a star is at the zenith.
But at any other position, the star is apparently raised; the effect is greatest at the horizon.

Define the angle of refraction R by R = z - z'.
Rearrange as z = R + z'.
Then
sin(z) = sin(R) cos(z') + cos(R) sin(z').

Assume R will be small, so, approximately,
sin(R) = R (in radians),
cos(R) = 0.

Thus, approximately,
     sin(z) = sin(z') + R cos(z').
Divide throughout by sin(z') to get
     sin(z)/sin(z') = 1 + R/tan(z')
which is to say,
     v0/vn = 1 + R/tan(z').
So we can write
     R = (v0/vn - 1) tan(z')
         = k tan(z').

Here v0 is c, the velocity of light in a vacuum, which is constant.
But vn depends on the temperature and pressure of the air at ground level.
At "standard" temperature (0°C = 273K) and pressure (1000 millibars),
     k = 59.6 arc-seconds.
The formula in the Astronomical Almanac is
     k = 16.27" P(millibars)/(273+T°C)

At large zenith distances, this model is inadequate.
The amount of refraction near the horizon is actually determined observationally.
At standard temperature and pressure,
refraction at the horizon (horizontal refraction) is found to be 34 arc-minutes.

Previous section.

Next section.

Return to index.