Enakostranični trikotnik 1. (stranica trikotnika) 2. 3. 4.
Podatki :
  • enakostraničnost,
  • stranica trikotnika {a}
    		•
    Težavnost :
    Veljavnost:

    		 I
    {es.sa.__}
     

    1.korak

  • vodoravno načrtamo daljico AB v dolžini {a}

    • 2.korak

  • vzamemo v šestilo razdaljo stranice {a}
  • iz točke A načrtamo lok nad sredino stranice AB
  • iz točke B načrtamo lok nad sredino stranice AB
  • v presečišču lokov dobimo točko C

    • 3.korak

  • načrtamo stranico BC
  • načrtamo stranico AC

    • 4.korak

  • uredimo oznake trikotnika

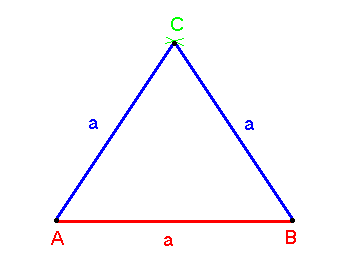
    • Naloga je vedno rešljiva !
    Načrtujemo po 1. skladnostnem izreku.     		Vrnitev Nad njim Prejšnji Naslednji Nazaj Naprej Na dno Na vrh Pomoč




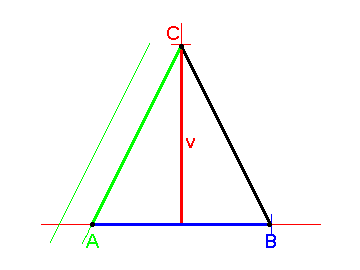
    Enakostranični trikotnik 1. 2. (višina, težiščnica) 3. 4.
    Podatki :
  • enakostraničnost,
  • višina trikotnika {v}
    		•
    Težavnost :
    Veljavnost:

    		 II
    {es.va.__}
     

    1.korak

  • vodoravno načrtamo nosilko daljice AB
  • navpično načrtamo nosilko višine na stranico AB
  • na navpičnici odmerimo dolžino višine {v} in točko C

    • 2.korak

  • na levi narišemo pomožno premico pod kotom 60°
  • skozi C načrtamo vzporednico s pomožno premico
  • v presečišču dobimo točko A

    • 3.korak

  • zapičimo šestilo v A, odmerimo razdaljo do C
  • zavrtimo šestilo na vodoravnico in določimo točko B

    • 4.korak

  • načrtamo stranico BC ojačamo drugi dve
  • označimo trikotnik

    • Naloga je vedno rešljiva !
    Upoštevamo lastnosti višine in enakost kotov 60°.
    Težiščnica je ista daljica kot višina.     		Vrnitev Nad njim Prejšnji Naslednji Nazaj Naprej Na dno Na vrh Pomoč





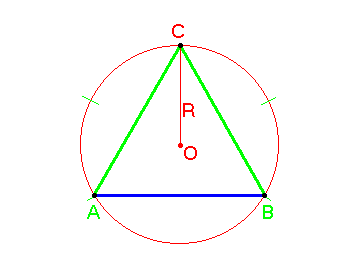
    Enakostranični trikotnik 1. 2. 3. (polmer očrtane krožnice) 4.
    Podatki :
  • enakostraničnost,
  • polmer očrtane krožnice {r}
    		•
    Težavnost :
    Veljavnost:

    		 I
    {es.po.__}
     

    1.korak

  • izberemo točko O in načrtamo krožnico s polmerom {r}

    • 2.korak

  • na vrhu krožnice si izberemo točko C
  • na levo po krožnici odmerimo dvakrat razdaljo {r}
  • dobimo točko A, načrtamo stranico AC
  • na desno po krožnici odmerimo dvakrat razdaljo {r}
  • dobimo točko B, načrtamo stranico BC

    • 3.korak

  • načrtamo krak AB

    • 4.korak

  • ojačamo stranice in označimo trikotnik

    • Naloga je vedno rešljiva !
    Upoštevamo, da polmer {r}
    razdeli krožnico na šest delov.     		Vrnitev Nad njim Prejšnji Naslednji Nazaj Naprej Na dno Na vrh Pomoč




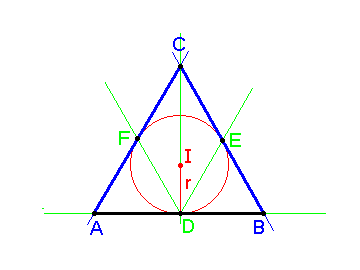
    Enakostranični trikotnik 1. 2. 3. 4. (polmer včrtane krožnice)
    Podatki :
  • enakostraničnost,
  • polmer včrtane krožnice {r}
    		•
    Težavnost :
    Veljavnost:

    		 II
    {es.pv.__}
     

    1.korak

  • načrtamo krožnico s polmerom r, središče označimo z I

    • 2.korak

  • načrtamo navpičnico skozi točko I
  • v spodnjem presečišču s krožnico dobimo točko D
  • skozi točko D potegnemo pravokotnico na premico DI
  • iz točke D potegnemo v desno premico pod kotom 60°
  • v presečišču s krožnico dobimo točko E
  • iz točke D potegnemo v levo premico pod kotom 60°
  • v presečišču s krožnico dobimo točko F

    • 3.korak

  • skozi točko E potegnemo vzporednico premici DF
  • v presečišču z vodoravnico dobimo točko B
  • v presečišču z navpičnico dobimo točko C
  • narišemo premico skozi točki C in F
  • v presečišču z vodoravnico dobimo točko A

    • 4.korak

  • ojačamo stranice in označimo trikotnik

    • Naloga je vedno rešljiva! Upoštevamo lastnost
    enakostraničnega trikotnika, da so točke DEF
    hkrati razpolovišča, nožišča in dotikališča.     		Vrnitev Nad njim Prejšnji Naslednji Nazaj Naprej Na dno Na vrh Pomoč