Serwey: Physics for Scientiests and Engineers, Vol. 1. Third edition

ESSEY

Galloping Gertie: The Tacoma Narrows Bridge Collapse

Robert G. Fuller, University of Nebraska - Lincoln

Dean A. Zollman, Kansas State University

The Tacoma Narrows Bridge was not the first suspension bridge to collapse. In fact,a survey of the history of suspension bridges shows that several were destroyed by wind or other oscillating forces (Table 1).

However, the Tacoma Narrows Bridge was by far the longest and most expensive suspension bridge to collapse as a result of interaction with the wind. Perhaps this collapse seemed so striking because nearly 50 years had elapsed since the previous eollapse of a bridge.

At the time of the Tacoma Narrows Bridge collapse in 1940, many theories were advanced to explain what had happened. What follows are excerpts from six different explanations. Each presents a slightly different view of the role of design and wind factors in the collapse.

Why Did The Tacoma Narrows Bridge Collapse2(Six Theories)

It is very improbable that resonance with alternating vortices plays an important role in the oscillations of suspension bridges. First, it was found that there is no sharp correlation between wind velocity and oscillation Erequency such as is required in case of resonance with vortices whose frequency depends on the wind velocity. Secondly, there is no evidence for the formation of alternating vortices at a cross section similar to that used in the Tacoma Bridge, at least as long as the structure is not oscillating. It seems that it is more correct to say that the vortex formation and frequency is determined by the oscillation of the structure than that the oscillatory motion is induced by the vortex formation. A Report to the Honorable John M. Carmody, Administrator, Federal Works Agency, Washington, D. C. March 28,1941.

The primary cause of the collapse lies in the general proportions of the bridge and the type of stiffening girders and fioor. The ratio of the width of the bridge to the length of the main span was so much smaller and the vertical stiffness was so much less than those of previously constructed bridges that forces heretofore not considered became dominant. Board of Investigation, Tacoma Narrows Bridge, L.J. Sverdrup, Chairman, June 26, 1941.

Once any small undulation of the bridge is started, the resultant efiect of a wind tends to cause a building up of vertical undulations. There is a tendency for the undulations to change to a twisting motion, until the torsional oscillations reach destructive proportions. Bridges and Their Builders, D. Steinman and S. Watson, Putnam's Sons, N.Y., 1941.

The experimental results described in a (1942) report indicated rather definitely that the motions were a result of vortex shedding. University of Washington Engineering Experiment Station Bulletin No.116,1952.

TABLE 1 Collapsed Suspension Bridges 

Bridge                Designer        Span Length (ft)   Failure Date
Dryburgh (Scotland)   J. and W. Smith    260                1818
Union (England)       Sir Samuel Brown   449                1821
Nassau (Germany)      L. and W.          245                1834
Brighton (England)    Sir Samuel Brown   255                1836
Montrose (Scotland)   Sir Samuel Brown   432                1838
Menai (Wales)         T. Telford         580                1839
Roche (France)        LeBlanc            641                1852
Wheeling (USA)        C. Ellet           1010               1854
Niagara (USA)         E. Serrell         1041               1864
Niagara (USA)         S. Keefer          1260               1889
Tacoma Narrows        L. Moisseff        2800               1940

Summing up the whole bizarre accident, Galloping Gertie tore itself to pieces, because of two characteristics:1. It was a long, narrow, shallow, and therefore very flexible structure standing in a wind ridden valley; 2. Its stiffening support was a solid girder, which, combined with a solid floor produced a cross section peculiarly vulnerable to aerodynamic effects. Bridges andž Men, ). Gies, Doubleday and Co.,1963.

Aerodynamic instability was responsible for the failure of the Tacoma Narrows Bridge in 1940. The magnitude of the oscillations depends on the structure shape, natural frequency, and damping. The oscillations are caused by the periodic shedding of vortices on the leeward side of the structure, a vortex being shed first from the upper section and then the lower section. Wind Forces on Buildings and Structures, E. Houghton and N. Carruthers, ). Wiley dJ Sons, N.Y. 1976.

Physical Principles

The general principle of the Tacoma Narrows Bridge collapse is straightforward: a resonance eflect. However, the details of the physical mechanisms involved are neither trivial nor obvious.

Every system has a natural fundamental vibration frequency. If forces are exerted on that system at the right frequency and phase, sympathetic vibrations can be excited (see Section 13.7). Oscillating forces at the right frequency and phase can cause sympathetic vibrations of catastrophic proportions. The forces applied to the bridge by the wind were applied at a natural frequency of the bridge. Thus, the amplitude of the bridge's oscillations increased until the steel and concrete could no longer stand the stress.

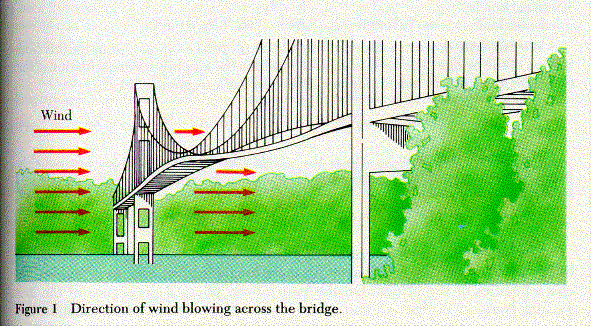
But how does the fluctuating force ofjust the right frequency arise as the wind blows across the bridge? The first idea that comes to mind is that the gusty wind arrived in pulses, thereby striking the bridge at just the appropriate frequency to cause the large oscillations. Closer examination of this explanation shows it cannot be correct. While all wind speeds fluctuate, these fluctuations tend to be random in phase and variable in frequency. Wind gusts are not the answer. Furthermore, the kinds of forces that must be exerted on the bridge are vertical forces-transverse to the direction of the wind. The wind was blowing across the bridge (from side to side, as shown in Figure 1), while the forces on the bridge were acting vertically. These oscillating vertical forces can be explained by a concept called vortex shedding. When a wind that exceeds a minimum speed blows around any object, vortices will be formed on the back side of that object (see Figure 2).

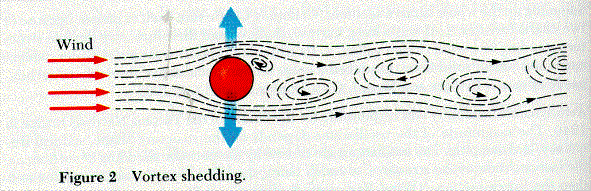
As the wind increases in speed, the vortices form on alternate sides of the downwind side of the object, break loose, and fiow downstream. At the time a vortex breaks loose from the back side of the object, a transverse force is exerted on the object. The frequency of these fiuctuating eddies is about 20% of the ratio of the velocity of the wind to the width of the object. These lateral forces can be as much as twice as large as the drag forces. Thus, vortex shedding allows us to understand the origin of the fiuctuating vertical forces on the Tacoma Narrows Bridge even though the wind was blowing across it in a transverse, horizontal direction.

Model of the Tacoma Narrows Bridge

Let us create a model of the Tacoma Narrows Bridge and treat it as if it were suspended by two springs with equal force constants, as shown in a cross-sectional view in Figure 3.

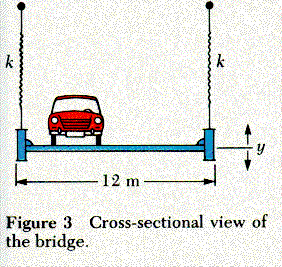
We can then write down the equations of motion using Newton's second law for translation (Eq.1) and for rotation (Eq. 2).

Mar = -k (yl + y2)

Ia = - (y2 - y1)

We then make a small angle approximation (Eq. 3)

q = (y2-y1)/W

and assume simple harmonic motion forms for the solutions to the simultaneous equations. Thus, we can write the solutions as:

y1 = A1 sin(w t) and y2 = A2 sin(w t.)

We can write down in a standard way the two normal mode solutions for this cross section of the bridge. The vertical motion in which the amplitudes of oscillation of the two sides are equal in magnitude and direction has a frequency, wv,

w12 = w22 = wv2 = 2k/M (for A1= A2)

The torsional motion in which the amplitudes of the two sides are equal in magnitude but opposite in direction and has a frequency wt, where wt is given by

wt2 = w12 = w22 = kW2/(2MR2) (for A1= -A2)

The latter frequency describes the twisting motion that ultimately caused the bridge to fall down. The exact values for these oscillation frequencies depend on the characteristics of the bridge. On the basis of the physical properties of the first Tacoma Narrows Bridge, we find that the values appropriate for this analysis are: mass per unit length = 4.3 . 103 kg/m, width of the bridge =12 m, radius of gyration of the bridge = 4.8 m, effective spring constant =1.5 . 103 N/m. These numerical values result in the vertical normal mode frequency of 8 cycles per minute and the torsional motion of 10 cycles per minute. The approximate equality of these two frequencies played an important role in the fate of the Tacoma Narrows Bridge.

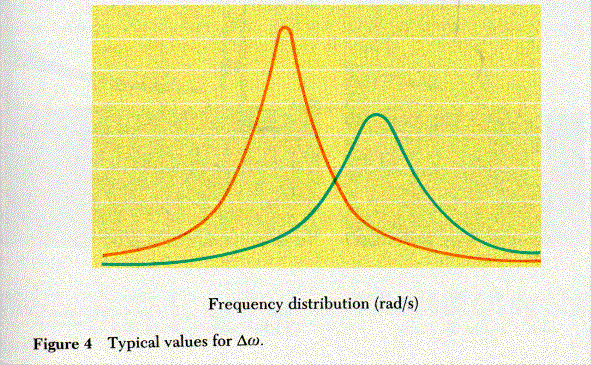
In a real system the normal mode frequency will not be a single frequency, but rather a distribution of frequencies. The energy per unit time that is accepted by a mode of oscillation is given by the following equation:

P(w) = [(w-w0)2 + (Dw/2)2]-1

were Dw is the width of the resonance response curve at half maximum. The maximum increases with the tendency of the system to resist oscillations. For the original Tacoma Narrows Bridge, the tendencies of the bridge to resist vertical and rotational, or torsional, motions were diferent. Hence the P(w) function for vertical and torsional motion has different values for w0, the normal mode frequency and for Dw Using the constants given above the values for wv, and wt, for vertical and torsional motion can be computed. Graphs of P(w)v and P(w)t versus w using typical values for Dw are shown in F”gure 4. The area of overlap of the two curves indicates the tendency of the vertical motion to pump energy into the rotational motion.

As can be seen in Table 2, the ratio of torsional to vertical frequencies for other long bridges is significantly larger than the ratio for the first Tacoma Narrows Bridge.

TABLE 2 Ratio of Torsional to Vertical Frequencies in Suspension Bridges 

Bridge           Length (m)  fv(1/min)   ft(1/min)  Ratio ft/fv
Verrazano          4260       6.2          11.9        1.9
Golden Gate        4200       5.6          11.0        1.9
Severn             3240       7.7          30.6        3.9
Tacoma Narrows 1st 2800       8.0          100         125

Even before the Tacoma Narrows Bridge was opened, the vortex shedding forces were pumping energy into the vertical motion of the bridge. Vertical oscillations were noticed early, and many people avoided using the bridge. However, the tor- sional oscillations did not occur until the day of the collapse. On that day a mechanical failure allowed the torsional oscillations to begin. Because this motion was closely coupled to the vertical motion of the bridge, it quickly led to its destruction. The photographs (Fig. 5) show the collapse of the Tacoma Narrows Bridge and provide a vivid demonstration of mechanical resonance.

Public Perceptions

It is interesting to recall some public perceptions involving the bridge collapse. Locals had already noticed for some time that, when driving across this technological marvel, they would experience an undeniable bounce. Some tried to deal with this humorously. For example, the bridge was often referred to as "Galloping Gertie."

An editorial in the Tacoma Times dated August 25,1940 (soon after the bridge was opened) made the following comment regarding the tolls being charged:

There is no truth to the rumor that part of the Narrows Bridge toll is for the scenic railway effects. The charge is for cross only and the bounce is free.

Before the Tacoma Bridge collapsed, bridges had been considered secure, so much so that a local insurance agent who had arranged a second 800,000 auxiliary policy on the bridge had never bothered to pay the premium. Instead, he pocketed the money and was sent to jail following the disaster.

The collapse of the Tacoma Narrows Bridge was a watershed in the design of suspension bridges. The debates as to who was responsible and whether anything could have been done to prevent the collapse continue.

Suggested Readings

Aerodgnamic Stability of Suspension Bridges University of Washington, Engineering Experiment Station Bulletin No. 116, Parts I, II, III, IV, and V, University of Washington Press, Seattle,1949,1950,1952, and 1954.

O'Connor, C. Design of Bridge Superstructures, New York, John Wiley 8z Sons,1971. The Failure of the Tacoma Narrows Bridge. A Reprint of Original Reports, School of Engineering, Texas Engineering Experiment Station, College Station, Texas, Bulletin No. 78,1944.

Fuller, Robert G. Dean Zollman, and Thomas C. Campbell, The Puzzle of the Tacoma Narrows Bridge Collapse, New York, John Wiley 8z Sons,1982.

Houghton E.L., and N.B. Carruthers, Wind Forces on Buildmgs and Structures: An Introduct on, New York, Halsted Press,1976.

Scigliano, Eric, "Galloping Gertie," Pacific Northwest, January 1989.

Simiu, E., and R.H. Scanlan, Wind Ežects on Structures: An Introduction to Wind Eng”neering, New York, John Wiley Hž Sons,1978.

Steinman, D.B., Šuspension Bridges: The Aerodynamic Problem and its Solution," American Scientist, July 1954, pp. 397-438.

Wind Efects on Bridges and Other Flexible Structures, Notes on Applied Science, No. 1, National Physics Laboratory, London,1955.

Essay Questions

1. The Tacoma Narrows Bridge was a two-lane bridge. How would the bridge have behaved had it been a four-lane bridge?

2. Based on current knowledge, what would have been your advice for a "quick fix" for the bridge which could possibly have averted the d”saster?

Essay Problems

1. Calculate the effect of stiffening the bridge suspension by increasing the effective spring constant of the Tacoma Narrows Bridge by 50%.

2. How much change in the total mass of the Tacoma Narrows Bridge is necessary to bring the vibrational frequency down to that of the Golden Gate BridgeP Assume uniform mass distribution.