Uaznáčma s fn šteuila zajčih párau na začíetku n -tga mísca, číer je n = 0, 1, 2, 3, ... . Na začíetku ta prejga mísca je an pár, zatú je f1 = 1. Pár je star an mísc. Čez an mísc zajka kati nau pár, de sta na začíetku ta drujga mísca duá pára. Čez an mísc ma ta prej pár spíet mláde, da nau pa še ne, tak de sa na začíetku ta trejčga mísca že trije pári. Tú se práj: f2 = 2, f3 = 3. Čez an mísc, tú se práj na začíetku ta četo'rtga mísca, ma ta prej pár spíet máde, ta druj pa tut, ka j star že duá mísca, le ta trejč pár še ne, kár pamin, de je f4 = 5. U n -tmu míscu bo na tá uiža tulkáj zajčih párau, kuko'r ih je blu u (n - 1) -jmu mpa u (n - 2) -jmu ukop. Po'r tem je seuíde n > 2.
Dabil sma:
fn = fn-1 + fn-2, f1 = 1, f2 = 2.
Usák uatrak, ka zná seštíuat, bo zračunau, de greje ta šteuila kujst:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
Na začietku duanajstga mísca bo 233 zajčih párau.
Kulk nejč ih je bel patle? A se na dá tu zračunat bel pačíes? Kadu bo pa kar naprej seštíuau! Formula je, u ne pa nastuop zlátu razmíerje
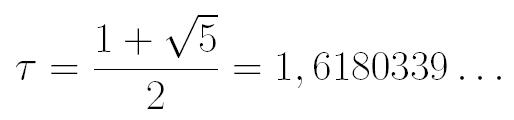
Tega pamnažima (n + 1) -kat sámga s sába, rezultát delima s karejnem uat 5, názadne pa je fn narbliži cílu šteuila uat tistga, kár sma prej dabil.
Panauát šteuila Bonáčejga púba uaznačujema s Fn za n = 0, 1, 2, 3, ... . Zajne uelá
Fn = Fn-1 + Fn-2, F0 = 0, F1 = 1.
Zatú je fn = Fn+1.