Dne 3. 4. 1998 je bilo na šoli organizirano Izbirno tekmovanje iz matematike.
Na tekmovanje se je prijavilo15, tekmovalo pa 14 učencev. Četrti letniki
niso tekmovali.
Doseženi rezultati po letnikih in uspehu:
| Dijak (inja) |
Letnik |
Mentor |
Doseženo mesto |
| Brunskole Irena |
1 |
J. Pavlišič |
1 |
| Skube Peter |
1 |
J. Pavlišič |
2-3 |
| Kuzma Tomaž |
1 |
J. Pavlišič |
2-3 |
| Kramarič Anja |
1 |
J. Pavlišič |
4 |
| Grabrijan Uroš |
1 |
J. Pavlišič |
5 |
| Šavli Jan |
1 |
J. Pavlišič |
6-7 |
| Rogina Primož |
1 |
J. Pavlišič |
6-7 |
| |
| Pavlišič Ana |
2 |
P. Skrbinšek |
1 |
| Brunskole Mojca |
2 |
P. Skrbinšek |
2 |
| Petruna Nina |
2 |
P. Skrbinšek |
3 |
| |
| Pavlišič Andrej |
3 |
V. Petruna |
1-2 |
| Kuretič Marko |
3 |
V. Petruna |
1-2 |
| Fabjan Rok |
3 |
V. Petruna |
3 |
| Pavlakovič Katarina |
3 |
V. Petruna |
4 |
IZBIRNO TEKMOVANJE IZ MATEMATIKE
NALOGE ZA PRVI LETNIK
Poišči vsa naravna števila, ki so enaka enajstkratniku
vsote svojih števk.
Dokaži, da je število 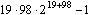 deljivo s 3.
deljivo s 3.
Meta je prestavljala kozarca valjaste oblike z zunanjima
premeroma 4 in 6 cm po papirju kvadratne oblike s stranico 9 cm. Če kozarca
primerno postavi, lahko vzdolž ene stranice papirnatega kvadrata odreže
pravokoten trak, pa bosta kozarca še zmeraj na papirju. Kolikšna je največja
širina traku, ki ga lahko odreže?
Na črno-beli šahovnici velikosti n x
n je prvo polje v prvi vrstici pobarvano črno. Janezek
je v vsaki sodi vrstici vsa bela polja pobarval modro. Dokaži naslednji
trditvi o tako pobarvani šahovnici:
(a) Šahovnica ima enako število modrih in belih polj.
(b) Šahovnica ima sodo mnogo črnih polj natanko tedaj,
ko je n sodo število.
NALOGE ZA DRUGI LETNIK
Pokaži, da enačba 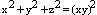 nima rešitev
v naravnih številih.
nima rešitev
v naravnih številih.
Za pozitivna realna števila a, b in c velja:
a + b - | a - b | - | a + b +
| a - b | -2c | > 0
Dokaži, da so a, b in c dolžine stranic nekega trikotnika.
Dan je pravokotnik ABCD z dolžinama stranic | AB | = 15
in | BC | = 10. V notranjosti pravokotnika leži taka točka E,
da je | DE | =12 in | CE | = 9. Izračunaj razdalji | AE
| in | BE |.
Janezek je, ko so doma kupili nov avto, na števcu kilometrov prebral
000052. Nato je ob vsakem prevoženem kilometru izačunal vsoto števk, ki
jih je pokazal števec. Nekega dne je prvič ugotovil, da vsota števk še
nikoli ni bila višja in da je bila že pred 9000 kilometri prav tolikšna.
Kaj je tistega dne prebral na števcu? Čez koliko prevoženih kilometrov
je bila vsota števk na števcu prvič večja od takratne?
NALOGE ZA TRETJI LETNIK
Naj bosta b > 1 in n > 1 taki naravni
števili, da je število 11...1(b) (n
enic), zapisano v številskem sistemu z osnovo b, praštevilo. Dokaži,
da je tudi n praštevilo.
Dana je kvadratna funkcija 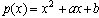 ,
kjer sta a in b poljubni celi števili. Pokaži, da za vsako
celo število n obstaja tako celo število m, da je
,
kjer sta a in b poljubni celi števili. Pokaži, da za vsako
celo število n obstaja tako celo število m, da je
p(n) p(n+1) = p(m)
Na stranici BC trikotnika ABC je izbrana
takšna točka D, da je | BD | = | AC | = 1 in
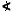 BAD = 1/3
BAD = 1/3 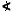 DAC
= 30°. Izračunaj dolžino daljice CD.
DAC
= 30°. Izračunaj dolžino daljice CD.
Dvanajst oseb se je usedlo k pojedini za okroglo mizo, vendar se nobeden
od njiju ni usedel na mesto, ki mu ga je bil določil gostitelj. Dokaži,
da se lahko krožno presedejo tako, da bosta vsaj dve osebi sedeli na pravih
mestih.
NALOGE ZA ČETRTI LETNIK
Pokaži, da ne obstajajo naravna števila l, m in
n, ki zadoščajo enačbi 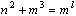 .
.
Naj bo 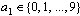 poljubno število. Za vsak n
poljubno število. Za vsak n 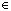 N
označimo z
N
označimo z 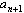 zadnjo
števko števila
zadnjo
števko števila 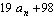 v desetiškem zapisu. Dokaži, da je
v desetiškem zapisu. Dokaži, da je 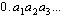 racionalno število.
racionalno število.
Naj bo H višinska točka in T težišče takega
ostrokotnega trikotnika ABC, v katerem je daljica HT vzporedna
stranici AB. Dokaži, da je tg 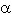 · tg ß = 3, kjer smo z
· tg ß = 3, kjer smo z 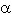 označili notranji kot pri ogljišču A in z ß notranji kot
pri ogljišču B.
označili notranji kot pri ogljišču A in z ß notranji kot
pri ogljišču B.
- Neko pleme ima 90 vojščakov in vsak izmed njih ima sulico,
okrašeno z devetimi rdečimi ali zlatorumenimi peresi rajske ptice. Peresa
so na vsako sulico pritrjena zaporedoma in nobeni dve rdeči peresi nista
sosednji. Ali imajo lahko vsi vojščaki različno okrašene sulice?

![]() deljivo s 3.
deljivo s 3.