VPRAŠANJA ZA USTNI IZPIT IZ MATEMATIKE

ŠTEVILSKE MNOŽICE

1.      Naštejte vse lastnosti osnovnih računskih operacij v množici naravnih števil.

Izračunajte na vsaj dva načina vrednosti izrazov 4+13+7+6 in 24525 ter 217+817

2.      Definirajte pojma praštevilo in sestavljeno število. Kam sodi število l? Naštej kriterije
za deljivost z: 2, 3, 4, 5, 6, 8, 9.

Ugotovi s katerimi od naštetih števil je deljivo število 295674.

3.      Definirajte največji skupni delitelj in najmanjši skupni večkratnik dveh celih števil.
Kako ju lahko izračunamo? Kdaj sta si števili tuji?
Poiščite največji skupni delitelj in najmanjši skupni večkratnik števil 84 in 270

4.      Povejte razloge za vpeljavo celih števil. Navedite osnovne računske operacije v
množici celih števil in njihove lastnosti.

5.      Opišite urejenost celih števil (na številski premici) . Naštejte pravila za računanje z
neenakostmi.
Rešite neenačbo:   3(x - 8) < 4x + 6

6.      Kako je sestavljena množica celih števil?
Zapišite množico vseh:

a.      sodih celih števil

b.      lihih celih števil

c.      večkratnikov danega naravnega števila

Zapišite množico vseh večkratnikov števila 7 in množico vseh celih števil, ki dajo pri deljenju s 5 ostanek 4 .

7.      Razloži kako razstavljamo algebrske izraze.

 16a2 -25 =,   a2 -3a -10 =,   5a3 -5a =,   x3 -5x2 - 4x + 20 =

8.      Zapiši pravili za kvadrat in kub dvočlenika: (a ± b)2   in   (a ± b)3 .   Kako razstavimo
vsoto in razliko kubov a3 ±  b3 ?
Izračunaj: (4x + 3y)2 =,   (2x -1)3 =

9.      Kaj je ulomek? Kdaj sta ulomka enaka? Definirajte računske operacije z ulomki.

Izračunajte vrednost izraza:

10.   Primerjajte po velikosti dva ulomka. Zapišite nasprotno in obratno vrednost ulomka  . Ali je to vedno mogoče? Uredite po velikosti ulomke:  

11.   Kako racionalno število zapišemo v decimalni obliki? Kdaj je ta zapis končen?
Zapišite v decimalni obliki:   in    !

12.   Kaj je procent? Kaj je promil? Razložite povečanje oziroma zmanjšanje dane količine a za p%
Cena izdelka se je najprej povečala za 10 %, nato pa še za 5 %. Koliko odstotna je bila celotna podražitev ?

13.   Definirajte absolutno vrednost števila a.
Izračunaj:

 

PRAVOKOTNI KOORDINATNI SISTEM V RAVNINI

14.   Opišite pravokotni koordinatni sistem v ravnini in izpeljite formulo za računanje razdalje med dvema točkama.
Izračunajte razdaljo med točkama A(-2,3) in B(l,-l).

15.   Kako izračunamo ploščino trikotnika, ki leži v ravnini pravokotnega koordinatnega sistema? Kaj veste o orientaciji trikotnika?
Izračunajte ploščino trikotnika z oglišči A(2,3), B(1,5), C(4,1,).

 

LINEARNA FUNKCIJA, ENAČBA IN NEENAČBA

16.   Definirajte linearno funkcijo in povejte pomen konstant k in n. Kaj je njen graf?
Zapišite lineamo funkcijo za k = 2 in n = 3 ter narišite njen graf.

17.   Zapišite enačbo premice, ki poteka skozi dani točki A(x1, y1) in B(x2, y2). Razložite
pomen smernega koeficienta premice.
Zapišite enačbo premice skozi točki A(3, -2) in B(-l, 6) .

18.   Kaj veste o smernih koeficientih vzporednih (pravokotnih) premic?
Napišite enačbo premice, ki poteka skozi točko T(3, 2) in je vzporedna premici y = - 2x + 3.

19.   Kako izračunamo kot med premicama? Kdaj sta dve premici pravokotni, kaj vzporedni?
Izračunajte kot med premicama y = - 3x + 2 in

20.   Kaj je linearna enačba? Kako jo rešujemo? Koliko rešitev ima?
Rešite linearno enačbo:  (2x - l)2 - (x - 3).(x + 3) + 3x(2 - x) = 18

21.   Kako rešujemo linearne neenačbe z eno neznanko? Kaj so množice rešitev?
Rešite neenačbo x - 2 < 3x + 6 in utemeljite vse korake.

22.   Napišite implicitno, eksplicitno in odsekovno enačbo premice. Enačbe katerih premic
lahko zapišemo v teh oblikah?
Enačbo premice 3y - 2x + 6 = 0 preoblikujte v eksplicitno in odsekovno obliko.

 

SISTEM LINEARNIH ENAČB Z DVEMA NEZNANKAMA

23.   Kaj je rešitev sistema dveh linearnih enačb z dvema neznankama? Kako rešujemo
sisteme dveh linearnih enačb z dvema neznankama?
Rešite sistem:
2x + 3y = 8
3x - 2y = -1

24.   Zapišite sistem dveh linearnih enačb z dvema neznankama. Koliko rešitev ima?
Razložite njegov geometrijski pomen.
Izračunajte koordinati presečišča premic z enačbama x - 2y – 5 = 0 in 2x - 3y - 7 = 0 .

POTENCE IN KORENI

25.   Naštejte in utemeljite pravila za računanje s potencami z naravnimi eksponenti.
Poenostavite izraz:  a4 b2 (-2ab3) 5  .

26.   Definirajte potenco z negativnim celim eksponentom in naštejte pravila za računanje
s potencami s celimi eksponenti.
Poenostavite:   a-2 b3 (ab-4) -3  : (a-2 b 8)

27.   Razložite pomen negativnega cksponenta, eksponenta 0 in potenciranje potenc z
negativno osnovo.
Izračunajte x -l y + x y -l +x° =   in  (- 2)3 - (- 3)2 + (5 - 3)° =

28.   Definirajte potence z racionalnim eksponentom in razložite, kako z njimi računamo.
Izračunajte: ,   ,  

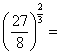
29.   Definirajte kvadratni koren in naštejte pravila za računanje s kvadratnimi koreni.
Izračunajte:  , 

30.   Definirajte n - ti koren. Naštejte pravila za računanje s koreni.
Poenostavite izraz:  

31.   Razložite racionalizacijo korenov?
Racionalizirajte:   in   


KVADRATNA FUNKCIJA, ENAČBA IN NEENAČBA

 

32.   Opišite graf kvadratne funkcije f(x) = ax2 + bx +c . Razložite pomen koeficientov a in c. Kje je teme grafa kvadratne funkcije?
Poiščite teme grafa funkcije f(x) = 2x2 - 8x + 7 in zapišite enačbo v temenski obliki.

33.   Kaj je kvadratna funkcija? Kaj je njeno dcfinicijsko območje? Naštejte tri najpogostejše oblike enačbe kvadratne funkcije in opišite pomen posameznih parametrov (konstant).

34.   Opišite graf kvadratne funkcije. Pojasnite pojme teme ter sečišča z abscisno in ordinatno osjo.
Narišite graf kvadratne funkcije f(x) = x2 + 3x -4.

35.   Opišite pomen diskriminante kvadratne funkcije in zapišite njeno enačbo.
V enačbi 8x2 + (2 - m)x + m - 8 = 0 določite m tako, da bo imela enačba med seboj enaki rešitvi.

36.   Zapišite kvadratno enačbo. Kako jo rešimo? Kako je z rešljivostjo v R?
Poiščite rešitve enačb 2x2 + 5x + 2 = 0 in x2 - 2x + 2 = 0.

37.   Povejte Vietovi formuli za kvadratno enačbo x2 + px + q = 0. Koliko rešitev ima kvadratna enačba in od česa je njihovo število odvisno?
Rešite enačbi:
a) x2 - 3x -10 = 0
b) 3x2 - 9x = 12

38.   Kako lahko določimo sečišča premice in kvadratne parabole?
Izračunajte, v katerih točkah se sekata premica y = 2x -1 in parabola y = -x2 + 2x + 3.

39.   Kako lahko določimo sečišča kvadratnih parabol?
Izračunajte, v katerih točkah se sekata paraboli y = -x2 + 1 in y = x2 + 2x — 3 .

40.   Kako rešujemo kvadratne neenačbe? Kaj je množica rešitev? Pomagajte si s sliko.
Poiščite rešitve neenačbe x2 - 7x +10 < 0 .

41.   V istem koordinatnem sistemu narišite grafe potenčnih funkcij za različne eksponente y = x-1, y = x-2 ,  y = x-3  in  navedite njihove lastnosti. Kaj imajo skupnega vse potenčne funkcije z negativnim eksponentom.

EKSPONENTNA IN LOGARITEMSKA FUNKCIJA

42.   Definirajte eksponentno funkcijo, narišite njen graf in opišite njene osnovne lastnosti.
Narišite grafa: y = 2x   in 

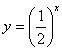
43.   Definirajte eksponentno enačbo in razložite, kako jih rešujemo.
Rešite enačbo:  .

44.   Definirajte logaritemsko funkcijo z osnovo a (a > l) in narišite njen graf. Določite njeno definicijsko območje in naštejte njene lastnosti.
Narišite graf: y = log 2 x

45.   Naštejte pravila za računanje z logaritmi.
Izraz log a + 2 log b - 3 log c zapišite kot logaritem enega izraza.

46.   Definirajte logaritemsko enačbo in povejte kako jo rešujemo.
Rešite enačbo log 5 – log (x +1) = log 3 - log x .

GEOMETRIJA V RAVNINI

47.   Kdaj sta si dva trikotnika podobna? Kaksna je povezava med stranicami, višinami, obsegom in ploščino podobnih si trikotnikov?
Stranice trikotnika ABC so v razmerju 3:5:7. Izračunajte obseg podobnega trikotnika A'B'C' katerega najkrajša stranica meri 9cm.

48.   Definirajte pojem: toga preslikava. Naštejte in opišite jih.
Trikotnik ABC zavrtite okoli poljubne točke C za kot 30o.

49.   Kaj je trikotnik? Kdaj so lahko tri števila dolžine stranic trikotnika? Kaj lahko poveste o kotih, ki ležijo tem stranicam nasproti?
Ali obstaja trikotnik s podatki:
a) a = 5cm, b = 7cm, c = 14cm ?
b) a = 9cm, c = 7cm, γ = 95° ?

50.   Opišite lastnosti enakostraničnega in enakokrakega trikotnika ter zapišite obrazca za ploščino. Ploščina enakokrakega trikotnika meri 38,88 dm2 , vc pa 5,4 dm. Izračunajte dolžini osnovnice c in kraka a.

51.   Kaj je paralelogram? Naštejte paralelograme in zapišite obrazec za ploščino paralelograma.
V paralelogramu meri stranica a = l cm, višina va = 9 cm. Koliko meri njegova ploščina?

52.   Definirajte trapez in enakokraki trapez ter naštejte njune lastnosti. Kaj je srednjica trapeza? Kako izračunamo ploščino trapeza?
Izračunajte ploščino trapeza z osnovnicama a = 10 m in c = 6 m ter višino v = 5 m.

53.   Opišite krog in krožni izsek ter zapišite obrazca za ploščino in obseg kroga. Naštejte vse možne medsebojne lege krožnice in premice.
Izračunajte ploščino kroga, če njegov obseg meri 10π

54.   Definirajte pojem kota in pojasnite izraze: krak, vrh, ničelni, pravi, iztegnjeni in polni kot, ostri in topi kot. Kako merimo kote?
Izrazite kot 37,48° v minutah in sekundah.

55.   Definirajte kotne funkcije v pravokotnem trikotniku s katetama a, b in hipotenuzo c ter izpeljite osnovne zveze med njimi.
V pravokotnem trikotniku meri kateta a = 6cm in kot a = 36°. Izračunajte dolžino hipotenuze.

56.   Navedite kosinusni izrek in Pitagorov izrek. Kdaj ju uporabljamo?
Izračunajte največji kot v trikotniku s stranicami a = 4cm, b = 5cm, c = 6cm.

57.   Povejte sinusni izrek. Kdaj ga uporabljamo?
V trikotniku s podatki a = 6cm, c = 9cm, γ = 76°  izračunajte kot α .

GEOMETRIJSKA TELESA

58.   Opišite pokončno prizmo povejte formuli za površino in prostornino.
Pravilna štiristrana prizma ima osnovni rob 8 cm višino 12 cm.Izračunajte prostornino
prizme.

59.   Opišite pokončno piramido povejte formuli za površino in prostornino.
Izračunajte površino enakorobne tristrane piramide z robom a = 6cm.

60.   Opišite pokončni valj povejte formuli za površino in prostornino.
Prostornina valja meri 280cm3, višina pa 7cm. Izračunajte površino.

61.   Opišite pokončni stožec povejte formuli za površino in prostornino.
Izračunajte prostornino stožca, če merita polmer r = 3cm in stranica s = 5cm.

62.   Opišite kroglo in povejte formuli za površino in prostornino krogle.
Kolikšni sta površina in prostornina krogle s polmerom r = 5cm?

KOTNE FUNKCIJE

63.   Definirajte funkcijo sinus za poljuben kot, narišite njen graf in naštejte njene lastnosti.
Narišite graf f(x) = 3 sin 2x.

64.   Definirajte funkcijo kosinus za poljuben kot, narišite njen graf in naštejte njene lastnosti.
Narišite graf f(x) = 2 cos 3x .

65.   Definirajte funkcijo tangens za poljuben kot. Določi njeno definicijsko območje in periodo.
Določite definicijsko območje in periodo funkcije f(x) = tg 3x.

66.   Razložite pojme periodičnost, sodost, lihost in jih obravnavajte pri funkcijah sinx, cosx in tgx.
Določite periodo funkcije f(x) = cos(3x) in preverite ali je funkcija soda (liha).

67.   Kaj pomeni, da je realna funkcija realne spremenljivke periodična? Kaj je osnovna perioda? Naštejte nekaj primerov periodičnih funkcij.
Kolikšna je perioda funkcije f(x) = sin(2x)?

POLINOMI IN RACIONALNE FUNKCIJE

68.   Definirajte potenčno funkcijo z naravnim (sodim, lihim) eksponentom. Opišite graf potenčne funkcije.
Narišite grafa za eksponenta n = 2, 3.

69.   Kaj je ničla realne funkcije realne spremenljivke? Opišite obnašanje grafa polinoma in racionalne funkcije v okolici ničel.
V kateri točki seka graf polinoma p(x) = 2(x - l)(x +1)2 (x - 2)3 abscisno os in v katerih se
je dotika?

70.   Opišite (brez utemeljitve oz. dokazovanja) Hornerjev algoritem in pojasnite njegovo
uporabnost.
S Homerjevim algoritmom preverite, če sta števili 2 in -3 rešitvi enačbe:
x3 + 6x2 – x – 30 = 0.

71.   Kako poiščemo cele ničle polinoma s celimi koeficienti?
Poiščite cele ničle polinoma p(x) = x3 - x2 - 5x - 3.

72.   Kaj je ničla polinoma (enkratna, večkratna)? Koliko ničel ima polinom n-te stopnje? Kako zapišemo polinom, če poznamo vse njegove ničle?
Zapišite polinom četrte stopnje z vodilnim koeficientom 2, ki ima enojni ničli 1 in 3 ter dvojno ničlo -2.

73.   Povejte osnovni izrek o deljenju polinomov. Opišite deljenje z linearnim
polinomom.
Poiščite količnik in ostanek pri deljenju polinoma 2x3 - 3x2 + 8x - 6 s polinomom x - 3.

74.   Razložite postopek risanja grafa polinoma. Kako vodilni koeficient in prosti člen vplivata na potek grafa polinoma? Kako se graf polinoma obnaša v okolici ničel?
Skicirajte graf polinoma p(x) = x3 -x2.

75.   Kje racionalna (polinomska) funkcija spremeni predznak? Kako rešujemo racionalne (polinomske) neenačbe?
Kje racionalna funkcija: 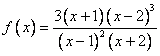 spremeni predznak?

76.   Definirajte racionalno funkcijo. Kaj je ničla in kaj pol racionalne funkcije? Kako se obnaša graf racionalne funkcije daleč od izhodišča? Kako se graf racionalne funkcije obnaša v bližini pola?
Skicirajte graf funkcije:  

77.   Pri katerih vrednostih x ima racionalna funkcija pole? Kaj se dogaja z grafom funkcije v bližini polov.
Poiščite pole racionalne funkcije  in opišite obnašanje grafa v bližini pola.

78.   Razložite pojem asimptota racionalne funkcije in kako jo izračunamo.
Izračunaj asimptote funkcij:  ;  :  .

79.   Kako rešujemo racionalne neenačbe? Kaj je njihova rešitev? Reši neenačbo:

ZAPOREDJA

80.   Kaj je zaporedje? Kdaj narašča (pada), kdaj je omejeno?
Obravnavaj zaporedje

81.   Opišite graf zaporedja. Kaj sta zgornja in spodnja meja zaporedja?
Narišite graf zaporedja an = 2x -1. Ali ima zaporedje spodnjo in zgornjo mejo?

82.   Kdaj je zaporedje aritmetično? Zapišite splošni člen in obrazec za vsoto prvih n členov. Kaj je aritmetična sredina dveh števil?
Ali je zaporedje  aritmetično? Če je, zapišite splošni člen.

83.   Kdaj je zaporedje geometrijsko? Zapišite splošni člen in vsoto prvih n členov. Kaj je geometrijska sredina dveh pozitivnih števil?
Določi x tako, da bo zaporedje x, x + l, x -3 geometrijsko.

OBRESTNO OBRESTNI RAČUN IN STATISTIKA

84.   Razložite pojme glavnica, obresti, obrestna mera, navadno in obrestno obrestovanje. Zapišite osnovni obrazec obrestno obrestnega računa.
Izračunajte na kolikšno vrednost naraste glavnica 300 000 SIT v 4 letih pri obrestni meri 6% in letni kapitalizaciji obresti.

85.   Razložite pojme obrestno obrestovanje, amortizacija, renta.
Vsako leto na začetku vložimo znesek 50 000 SIT. Kolikšna je vrednost vseh vlog na koncu tretjega leta, če je obrestna mera 8 % ob letni kapitalizaciji obresti?

86.   Razložite pojme populacija, statistična enota, vzorec, statistična spremenljivka.
Gornje pojme razložite na primeru uspeha posameznega dijaka v vašem razredu.

87.   Na kakšne načine lahko prikažemo večje količine podatkov? Razložite pojma absolutna in relativna frekvenca.
V razredu s 30 dijaki so bili ob koncu leta 4 odlični. Izračunajte absolutno in relativno frekvenco.

88.   Kaj je histogram?
V razreduje 24 dijakov. Pri šolski nalogi sta dva učenca dobila po 10 točk, štirje so dobili po 9 točk, osem po 8 točk in šest po 7 točk. Prikažite doseženo število točk s histogramom.

89.   Kaj je frekvenčni kolač?
V razredu je 24 dijakov. Pri šolski nalogi sta dva učenca dobila po 10 točk, štirje so dobili po 9 točk, osem po 8 točk in šest po 7 točk. Prikažite doseženo število točk s frekvenčnim kolačem.

90.   Razložite pojma povprečna vrednost in standardni odklon.
V razredu s 30 dijaki so pisali šolsko nalogo.Dva dijaka sta pisala odlično, štirje prav dobro, deset dobro, osem zadostno in šest nezadostno. Izračunajte povprečno oceno in standardni odklon.