Zanima nas torej delež ploščine trikotnika znotraj pravokotnika v primerjavi s ploščino samega pravokotnika.

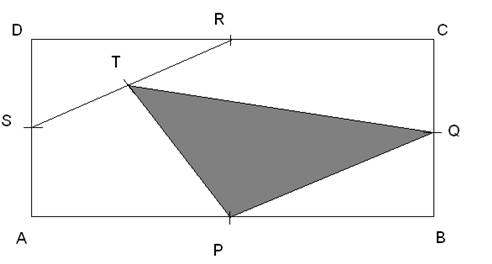
Ploščina pravokotnika je zelo enostavna in sicer je enaka produktu stranic. Če vzamemo, da je stranica AB=CD=a in stranica BC=DA=b, bi enačbo zapisali kot:

P=a*b

Kako priti do ploščine označenega trikotnika pa je drugo vprašanje. Ena izmed možnosti je, da si pomagamo s splošno enačbo za izračun ploščine trikotnika, ki se glasi takole:

Ptrikotnika= (a*Va)/2=(b*Vb)/2=(c*Vc)/2

(stranice a,b in c so v tem primeru mišljene kot stranice trikotnika in so različne od prej izbranih stranic za pravokotnik).

Žal je izračun preko slednje enačbe precej zakompliciran, se je zelo težko določiti pravokotnico na posamezno stranico. Vsaj eno stranico (PQ) bi sicer bilo relativno enostavno izračunati po Pitagorovem izreku …

Nekoliko lažji način izračuna ploščine je preko razlike in sicer:

Ptrikotnika=Ppravokotnika – Pnotranjosti brez trikotnika

Tako je potrebno določiti ploščino v pravokotniku, ki ni del označenega pravokotnika. Na videz težje zastavljena naloga, vendar če malce dorišemo par dodatnih črt, se stvari precej poenstavijo. Če med seboj povežemo razpolovišča sosednjih stranic, dobimo štiri identične like – pravokotne trikotnike s katetama (a/2) in (b/2). Ploščina enega takšnega trikotnika je torej:

P1=((a/2)*(b/2))/2=(a*b)/8

Ker imamo štiri takšne trikotnike, je ploščina vseh rumeno označenih likov:

4* P1= (a*b)/2

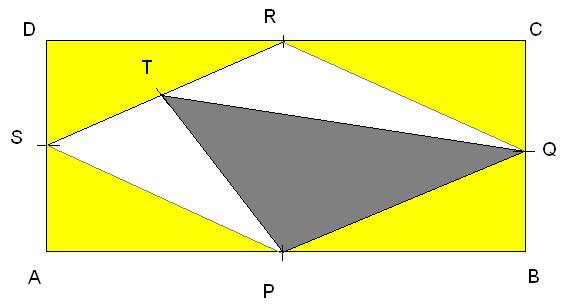
V kolikor smo sedaj pozorni, opazimo, da prestali del površine predstavlja romb s stranico, ki je enaka hipotenuzi v pravokotnem trikotniku s stranicama (a/2) in (b/2). Iskana ploščina je del ploščine tega romba.

Morda ti ne bo težko sami priti do končne rešitve, če dobro razmisliš, kolikšen del ploščine romba je iskana ploščina.

Zanimiva je tudi pot, kako priti do ploščine tega romba.

Tukaj te puščam samo, ker sem prepričan, da to zmoreš.