DOKAZ PITAGOROVEGA IZREKA


Za poljubna tri pozitivna števila a, b in c, za katera velja a² + b²  = c², obstaja trikotnik s stranicami a, b in c. V vsakem takšnem trikotniku je kot med stranicama a in b pravi.

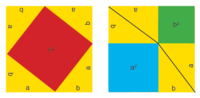
To trditev dokažemo s kosinusnim izrekom, ki je posplošitev Pitagorovega izreka za vse (evklidske) trikotnike, ne samo za pravokotne. Geometrijski dokaz izreka v obeh smereh lahko vidimo iz naslednje slike, kjer smo le preuredili rumene trikotnike, pa smo dobili enako preostalo površino kot prej (modre in zelene je skupaj ravno toliko kod rdeče).


                                    

<---- NAZAJ NA PRVO STRAN
<---- O PITAGORI
<---- ŠOLA FILOZOFIJE
<---- KAJ JE PITAGOROV IZREK
<---- PITAGOREJSKA TROJICA