MATEMATIKA

 

Programi za:

- delitelje:Delitelji3.exe

- prafaktorje:Prafaktorji.exe

- praštevila:Prastevila.exe

- največji skup...:Naj_D_v.exe

- period. decimalno št.: Periodno.exe

 

Avtor: S. Toplak

 

- Cabri geometrija.zip

 

Učitelji:

Jasmina Kumer

Slavko Toplak

Iris Breznik

Štefka Smej

 

Seminarske naloge iz matematike 8. razred

Seminarske naloge iz matematike 9. razred

Naloge za vajo (7. razred):

Naloge za vajo (8. razred):

Naloge za NPZ 9. razred:

MAT2004    MAT2005    MAT2006    MAT2008    MAT2009    MAT2010    MAT2011   MAT2012   MAT2013   MAT2014

Tekmovanje za Vegovo priznanje:

Šolsko tekmovanje

(bronasto priznanje)

 1. - 9. razred

četrtek, 16. marec 2017, ob 1300 (I.triada ob 1100)

Državno tekmovanje

(srebrno priznanje)

(zlato priznanje)

 5., 6., 7., 8., 9. razred

sobota, 22. april 2017, ob 900

 

Spletne povezave:

DMFA - Društvo matematikov, fizikov in astronomov Slovenije: http://www.dmfa.si/

( na tej strani se nahaja elektronska revija Brihtnež z mnogimi vsebinami za dodatno učenje matematike in kot priprava na tekmovanja )

 

Fakulteta za matematiko in fiziko:  http://www.fmf.uni-lj.si/

Pedagoška fakulteta Maribor: http://www.pfmb.uni-mb.si/

Presek: list za mlade matematike, fizike, astronome in računalnikarje:

http://zaloznistvo.dmfa.si/presek/

 

Zanimivosti:

Eulerjev izrek: "Za število vozlišč, daljic in ploskev velja naslednja zveza:  a + b - c = 1, kjer je
  • a - število vozlišč
  • b - število ploskev
  • c - število daljic oz. povezav

Za različne primere preveri veljavnost.

Podobna zveza velja za telesa. Razišči!

 

Številski sistemi: število 2005

1. Število 2005 v različnih številskih sistemih:

2005  =

 11111010101 [2]
  2202021 [3]
  133111 [4]
  31010 [5]
  13141 [6]
  5563 [7]
  3725 [8]
  2667 [9]
  1563 [11]
  505 [20]

Leto 2047 se bo v dvojiškem sistemu zapisalo s samimi enicami, in sicer:

         2047 [10] =  11 111 111 111 [2],

že naslednja letnica 2048 pa bo naslednje oblike:

        2048 [10] = 100 000 000 000 [2].

Iz zgornje tabele hitro najdemo še eno "lepo" številko, in sicer 2006 v trojiškem sistemu:

        2006 [10] = 2202022 [3]

2. Število 2005 kot razcep na prafaktorje:

        2005 = 5 . 401

3. Število 2005 kot razlika in vsota kvadratov:

        2005 = 2032 - 1982           ( ??? - hm, kako se pa to najde )                 

        2005 = 182 + 412

4. Zastavimo si nalogo in zapišimo število 2005 s samimi peticami (enicami,...). Tu navajam samo dve možnosti:

        2005 = 55-555-555-5-5

        2005 = 1111+11 . (1+1+1)1+1+1+1 +1+1+1

5.  Z malo truda  lahko pokažemo, da se 2005 ne da zapisati npr. kot:

        2005 = 12 + 22 + 32 + 42 + ...

        2005 = 11 + 22 + 33 + 44 + ...

Kmalu ali  že sedaj lahko začnemo raziskovati število 2006, čeprav ne iščemo v tem numeroloških ali astroloških zakonitosti, pač pa enostavno odkrivamo matematične zakonitosti. Le te so že same zase dovolj lepe.

( S. Toplak)

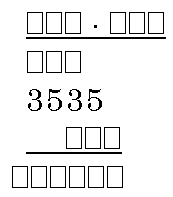
Naloga množenja

Videti je zahtevno, pa ni!

V nakazanem računu množenja zamenjaj kvadratke z desetiškimi števkami tako, da bo dobljeni račun pravilen.

 Rešitev:

- število 3535 je produkt prvega števila in sredinske števke drugega,  zato sta možnosti tu dve, in sicer: 3535:5=707 in 3535:7=505,

- prva in zadnja števka drugega ševila je 1, saj le tako dobimo produkt trimestno število,

- na koncu še premislimo o obeh možnostih; da so v rezultatu popolnjena vsa mesta, je edina možnost: 707 . 151 = 106757.

Število trikotnikov

Koliko trikotnikov je na sliki?

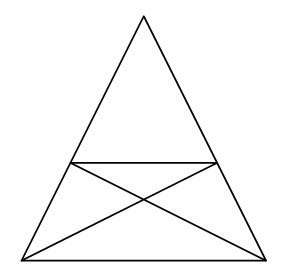Rešitev: 12 trikotnikov

 "Tablice so svetovne", učenci 8. razreda - skupina 2; 2014 (učilnica matematike)