Če se želite naučiti fizike, se morate najprej seznaniti z nekaterimi osnovnimi matematičnimi prvinami. V tem poglavju bomo pogledali nekaj matematičnih osnov.

Merske enote
Zapisovanje števil
Vrednostna števila
Grafi
Trigonometrija

Merske enote

Metrični merski sistem je standarden po vsem svetu. Tri bistvene enote, ki jih vsebuje so meter (m) za dolžino, sekunda (s) za čas in kilogram (kg) za maso.

100 centimetrov = 1 meter
3600 sekund = 60 minut = 1 ura
1000 gramov = 1 kilogram

Zapisovanje števil

Ko zapisujemo zelo visoka števila (npr. masa Zemlje) ali zelo nizka števila (npr. masa elektrona) uporabimo eksponentna števila. Osnovna oblika eksponentnega števila je X * 10

10^0 = 1
10^1 = 10
10^2 = 10 * 10 = 100
10^3 = 10 * 10 * 10 = 1000
10^-1 = 1 / 10 = 0.1
10^-2 = 1 / 10 / 10 = 0.01
10^-3 = 1 / 10 / 10 / 10 = 0.001

Maso Zemlje tako lahko zapišemo

6,000,000,000,000,000,000,000,000 kg = 6,0 *10^24 kg

Prav tako lahko zapišemo maso elektrona

0.000000000000000000000000000000911 kg = 9.11 * 10^-31 kg.

Vrednostna števila

Vrednostna števila so števila, ki imajo neko vrednost. Nekaj pravil:

Števila, ki niso enaka nič, so vedno vrednostna
Vse ničle, ki so zapisane za zadnjim številom, so vredostne
Ničle med ostalimi vrednostnimi števili so vedno vrednostne
Ničle, ki zapisujejo decimalno točko niso vrednostne

Pri seštevanju in odštevanju vedno zaokrožimo končni rezultat na nivoju najmanj natančnega člena:

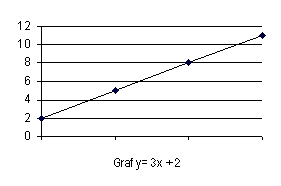
24.686 + 2.343 + 3.21 = 30.239 = 30.24

ker je 3.12 najmanj natančen člen.

Pri množenju in deljenju zaokrožimo rezultat na najmanjše število vrednostnih števil:

3.22 * 2.1 = 6.762 = 6.8

ker 2.1 vsebuje 2 vrednostni števili.

Pri problemu, ki vsebuje seštevanje, odštevanje, množenje in deljenje se rezultat zaokroži šele na koncu, ne vmes:

3.6 * 0.3 + 2.1 = 1.08 + 2.1 = 3.18 = 3.2

Grafi

V fiziki so najbolj pogoste tri vrste matematičnih funkcij

Ena od njih se imenuje linearno funkcija, ki jo lahko zapišemo z enačbo y=mx*b, kjer m določa nagnjenost funkcije, b pa točko, kjer funkcijo seka os y.

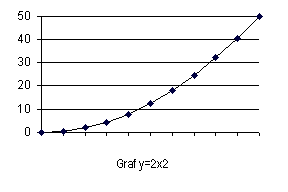
Druga funkcija se imenuje kvadratna funkcija. Enačba se glasi y=kx2, k pa je konstanta.

Tretja funkcija pa se imenuje inverzna funkcija, izražena z enačbo xy=k, kjer je k konstanta.

Trigonometrija

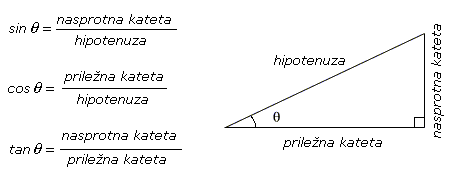
V fiziki je pomembna tudi trigonometrija, sploh kadar se ukvarjamo z vektorji. Nekaj pravil za izračunavanje kotov.