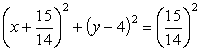KROŽNICA
Krožnica je množica točk v ravnini, ki
so za polmer oddaljene od izhodišča. Če imamo v koordinatnem sistemu krožnico
s polmerom r in središčem v
točki S(p,q), ima krožnica
enačbo 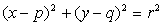
Med ostalimi stožnicami jo spoznamo po
tem, da sta koeficienta pred x2 in y2 enaka.

-
Določi središče in polmer krožnice z enačbo
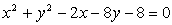 .
.
-
Kakšen polmer mora imeti krožnica
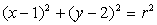 ,
da bo potekala skozi točko A(5,2) ?
,
da bo potekala skozi točko A(5,2) ?
-
Določi enačbo krožnice, ki se dotika obeh
koordinatnih osi in premice
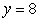 .
.
-
Določi enačbo krožnice, ki poteka skozi točki
A(–6,–2) in B(0,6), njeno središče pa leži na premici 4x+3y+6=0.
-
Določi enačbo krožnice, ki poteka skozi točki
A(3,1) in B(6,4), njeno središče pa je na y–osi.
-
Določi enačbo krožnice s središčem v presečišču
premic
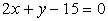 in
in 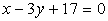 ,
če poteka skozi točko A(9,–5).
,
če poteka skozi točko A(9,–5).
-
Določi enačbo krožnice, ki poteka skozi točke
A(5,6), B(–3,2) in C(–2,–1).
-
Določi enačbo krožnice, ki poteka skozi točko
A(–7,9) in se dotika x–osi v točki B(–4,0).
-
Določi parameter k
tako, se bo krožnica
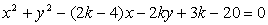 dotikala y–osi.
dotikala y–osi.
-
Določi parameter k tako, da se bo krožnica
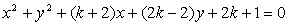 dotikala obeh koordinatnih osi.
dotikala obeh koordinatnih osi.
-
V katerih točkah seka krožnica
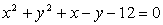 koordinatni osi ?
koordinatni osi ?
-
Določi enačbo nosilke tiste tetive v krožnici
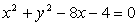 ,
ki jo točka A(1,1) razpolavlja.
,
ki jo točka A(1,1) razpolavlja.
-
Premica
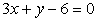 je sekanta krožnice
je sekanta krožnice 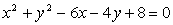 . Določi
dolžino ustrezne tetive in njen središčni kot.
. Določi
dolžino ustrezne tetive in njen središčni kot.
-
Skozi točko A(–1,y) na krožnici
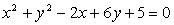 je konstruirana sekanta, ki je vzporedna s premico x–3y+7=0. Določi enačbo
te sekante in drugo presečišče.
je konstruirana sekanta, ki je vzporedna s premico x–3y+7=0. Določi enačbo
te sekante in drugo presečišče.
-
Določi enačbo krožnice, ki poteka skozi točki
M(10,9) in N(4,3), če je njeno središče na premici 2x–3y–6=0.
-
Kateri pogoj mora biti izpolnjen, da bosta
enačbi
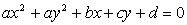 in
in  predstavljali koncentrični krožnici?
predstavljali koncentrični krožnici?
-
Poišči enačbo krožnice, ki je koncentrična
s krožnico
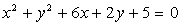 in poteka
skozi točko M(1,–4).
in poteka
skozi točko M(1,–4).
-
Določi enačbo krožnice, ki poteka skozi točki
C(3,4) in D(4,5), njeno središče pa je na krožnici
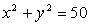 .
.
-
Določi enačbo krožnice s središčem v točki
S(3,–1), ki odseče na premici 2x–5y+18=0 tetivo dolžine 6.
-
Napiši enačbo krožnice, ki ima središče v
točki s(2,5) in se dotika krožnice
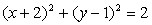
-
znotraj,
-
zunaj!
-
Določi enačbo krožnice, ki se dotika abscisne
osi v točki A(2,0) in se odzunaj dotika krožnice
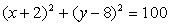 .
.
-
Določi enačbo krožnice, ki ima polmer r=5,
vsebuje točko M(8,7) in na abscisni osi odseče tetivo dolžine 6.
-
Določi enačbo krožnice, ki se dotika ordinatne
osi v točki N(0,10) in se odzunaj dotika krožnice
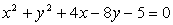 .
.
-
Določi lego točk A(–3,6), B(–2, 4) in C(1,3)
glede na krožnico
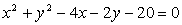 .
.
-
Določi lego premice glede na krožnico:
-
x+y–2=0 in (x–2)2+(y–1)2=25
-
x+y+4=0 in x2+y2–2y–3=0
-
4x+3y–36=0 in x2+y2–4x–2y–20=0
-
Določi medsebojno lego krožnic
-
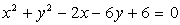 in
in 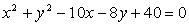 ,
,
-
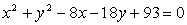 in
in 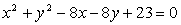 ,
,
-
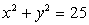 in
in 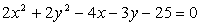
.
-
V enačbi premice y=kx+10
določi parameter k tako, da
bo tangenta krožnice
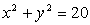 .
.
-
Določi parameter m tako, da
bo premica 2x+y+m=0 tangenta
krožnice
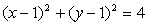 .
.
-
Določi enačbe tangent na krožnico
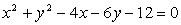 ,
ki so vzporedne s premico 4x–3y–12=0.
,
ki so vzporedne s premico 4x–3y–12=0.

rešitve
-
S(1,4); r=5
-
r=4
-
dve rešitvi
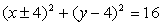
-
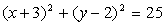
-
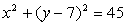
-
(x–4)2+(y–7)2=169
-
x2+y2–4x–4y–17=0
-
(x+4)2+(y–5)2=25
-
k1=6, k2=–2
-
k=4 ali k=0
-
A(0,–3), B(0,4), C(3,0), D(–4,0)
-
y=3x–2
-
Ö 10, 900
-
dve rešitvi:
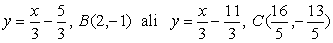
-
x2+y2–18x–8y+71=0
-
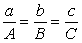
-
(x+3)2+(y+1)2=25
-
dve rešitvi: (x–7)2+(y–1)2=25 ali (x–1)2+(y–7)2=13
-
(x–3)2+(y+1)2=38
-
a) x2+y2–4x–10y+11=0 b) x2+y2–4x–10y–21=0
-
dve rešitvi: x2+y2–4x–10y+4=0 ali 9x2+9y2–36x+10y+36=0
-
dve rešitvi: (x–4)2+(y–4)2=25 ali (x–12)2+(y–4)2=25
-
dve rešitvi: x2+y2–5x–20y+100=0 ali
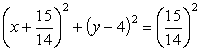
-
Točka A leži zunaj krožnice, točka B je na
krožnici, točka C pa je znotraj krožnice.
-
a) premica seče krožnico v točkah A(5,–39
in B(–2,4)
b) premica je mimobežnica
c) premica je tangenta v točki M(6,4)
-
a) krožnici nimata skupnih točk
b) krožnici se dotikata od zunaj v točki
A(4,7)
c) krožnici se dotikata odznotraj v točki
B(4,3)
d) krožnici se sekata v točkah A(4,2)
in B(3,–1)
-
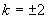
-
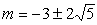
-
4x–3y–24=0 in 4x–3y+26=0

NAZAJ NA DOMAČO STRAN
NAZAJ NA ZAČETEK STOŽNIC
O.J.april 2001
![]()
![]()
![]()