Znanje v prahu
Nekaj malega teorije
 Na tej strani
je nekaj malega snovi, ki je potrebna za uspešno prebijanje skozi uganke
kralja Verjetnika..
Na tej strani
je nekaj malega snovi, ki je potrebna za uspešno prebijanje skozi uganke
kralja Verjetnika..
Upam, da se vsi skupaj zavedamo, da ta stran ne more nadomestiti kakšnega
poštenega učbenika (npr. J. A. Čibej: Matematika. Kombinatorika. Verjetnostni
račun. Statistika.).
Pravilo produkta (osnovni izrek kombinatorike): Kadar
lahko izbiranje opravimo v dveh fazah (izberemo to in
ono) in je število izbir v eni fazi neodvisno od izbora v drugi fazi,
dobimo število vseh izborov tako, da pomnožimo število izborov v eni fazi
s številom v drugi fazi. Pravilo lahko posplošimo na poljubno končno število
neodvisnih faz.
Pravilo vsote: Kadar lahko izbiramo
iz ene množice z n elementi ali iz druge
množice z m elementi in sta množici tuji (nimata skupnih elementov), dobimo
število vseh izborov tako, da seštejemo izbore v eni in tiste v drugi množici.
Tudi to pravilo lahko posplošimo na poljubno število množic.
Načelo vključitev in izključitev: Pri izbiranju
iz več množic moramo paziti, da je vsak element upoštevan natanko enkrat.
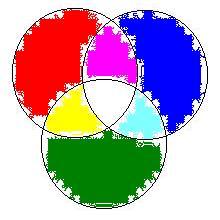 Kadar torej izbiramo
med elementi ene ali druge množice, pa se nekateri elementi lahko pojavijo
v obeh množicah (presek množic ni prazen), dobimo število vseh elementov
tako, da seštejemo št. elementov v prvi množici s številom tistih v drugi
in odštejemo število elementov v preseku (te smo te upoštevali dvakrat).
Kadar torej izbiramo
med elementi ene ali druge množice, pa se nekateri elementi lahko pojavijo
v obeh množicah (presek množic ni prazen), dobimo število vseh elementov
tako, da seštejemo št. elementov v prvi množici s številom tistih v drugi
in odštejemo število elementov v preseku (te smo te upoštevali dvakrat).
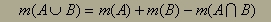
Če izbiramo med elementi treh množic, moramo najprej sešteti števila
elementov vseh posameznih množic, odšteti število elementov v presekih
po dveh množic in prišteti število elementov, ki nastopajo v preseku vseh
treh množic (te smo najprej trikrat prišteli, nato trikrat odšteli in jih
moramo torej še enkrat vključiti).
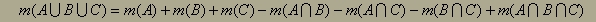
Analogno ravnamo, če se število množic še povečuje.
Permutacije: s to čudno tujo besedo označujemo
razporeditve vseh elementov neke množice v vrsto.Drug "tip nalog", pri
katerih uporabljamo permutacije, je tisti, ko oblikujemo urejene pare;
prvi element v paru iz prve množice in drugi iz druge množice. Množici
morata seveda imeti isto število elementov.
Permutacije brez ponavljanja - vsi elementi v množici so med
seboj različni . Naj jih bo n. Število takih razporeditev izračunamo tako,
da pomnožimo med seboj vsa naravna števila od n pa do 1. Ponavadi uporabimo
za to oznako !
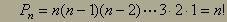 Permutacije s ponavljanjem - nekaterih elementov v množici med seboj
ne ločimo. Število teh razporeditev dobimo tako, da število vseh permutacij
delimo s permutacijami tistih, ki jih med seboj ne razlikujemo.
Permutacije s ponavljanjem - nekaterih elementov v množici med seboj
ne ločimo. Število teh razporeditev dobimo tako, da število vseh permutacij
delimo s permutacijami tistih, ki jih med seboj ne razlikujemo.
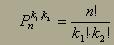 (če imamo dve skupini
enakih elementov)
(če imamo dve skupini
enakih elementov)
Variacije: v vrsto postavimo le nekaj elementov
iz množice, ki nam je na voljo.Recimo, da imamo n elementov, izberemo in
postavimo v vrsto pa jih le r (red variacije). Ponavadi lahko probleme
rešimo kar z uporabo pravila produkta. Če pa to ne gre, upoštevamo
Variacije brez ponavljanja - vsak element sme biti izbran samo
enkrat. 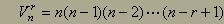 Zapomnimo si
raje, da je vseh faktorjev natanko r.
Zapomnimo si
raje, da je vseh faktorjev natanko r.
Variacije s ponavljanjem - vsak element lahko izberemo poljubno
mnogokrat. 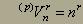
Kombinacije: elementov ne postavljamo v
vrsto, ampak samo delamo (oz. preštevamo podmnožice z zahtevanim številom
elementov - r red kombinacije)
Kombinacije brez ponavljanja - "prave" podmnožice, ker lahko
vsak element nastopa le enkrat v vsaki podmnožici. 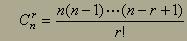
Kombinacije s ponavljanjem - niso podmnožice v pravem pomenu
te besede, ker lahko vsak element v njih nastopa tudi večkrat. Izračunamo
jih tako, da jih spremenimo v kombinacije brez ponavljanja po pravilu 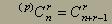
Število vseh podmnožic dane končne množice
z n elementi je 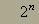 . Seveda
je ena med njimi prazna in ena celotna množica.
. Seveda
je ena med njimi prazna in ena celotna množica.


 Na tej strani
je nekaj malega snovi, ki je potrebna za uspešno prebijanje skozi uganke
kralja Verjetnika..
Na tej strani
je nekaj malega snovi, ki je potrebna za uspešno prebijanje skozi uganke
kralja Verjetnika..
 Kadar torej izbiramo
med elementi ene ali druge množice, pa se nekateri elementi lahko pojavijo
v obeh množicah (presek množic ni prazen), dobimo število vseh elementov
tako, da seštejemo št. elementov v prvi množici s številom tistih v drugi
in odštejemo število elementov v preseku (te smo te upoštevali dvakrat).
Kadar torej izbiramo
med elementi ene ali druge množice, pa se nekateri elementi lahko pojavijo
v obeh množicah (presek množic ni prazen), dobimo število vseh elementov
tako, da seštejemo št. elementov v prvi množici s številom tistih v drugi
in odštejemo število elementov v preseku (te smo te upoštevali dvakrat).
