KOMBINATORIKA
Pred vami je krajša zbirka nalog iz
kombinatorike. Nič posebnega, boste rekli, takih zbirk je kot listja in trave,
pa še rešitve imajo priložene.
Zakaj bi torej morali vzeti to zbirko v eno roko,
ter papir in svinčnik v drugo? Naloge, ki sledijo, namreč niso razdeljene po
poglavjih, kot smo jih obravnavali v šoli, ampak po objektih, ki v njih
nastopajo. Vsak mora torej sam ugotoviti, ali ima opravka s permutacijami,
variacijami, kombinacijami ali kakšnimi drugimi komplikacijami. Posebej so
zbrane le tiste naloge, kjer postopek reševanja ni zavit v skrivnost (načelo
vključitev in izključitev, binomski izrek).
Kdor se hoče preizkusiti na tak način, naj kar izvoli, ostalim pa ni treba nalog niti kopirati.
In rešitve? Teh zaenkrat ni. Pozorni bralec ali bralka pa seveda lahko naloge reši in jih pošlje v pregled. Mogoče bom nekega grdega dne (ob lepih dneh ne sedim za računalnikom) ravno njegove rešitve tudi objavil.
Pa veliko uspeha vam želi OJOJ.
november
2001
Številke
1) S ciframi 2, 3, 4, 5, 6 in 8 sestavljamo 4-mestna števila.
a) Koliko je vseh takih števil, če se cifre lahko ponavljajo?
b) Koliko jih ni deljivih s 25?
2) S ciframi 1,2,3,4,5,6,7 sestavljamo štirimestna števila.
a) Koliko je vseh takih števil, če se cifre lahko ponavljajo?
b) Koliko števil je sodih, če se cifre ne smejo ponavljati?
c) Koliko se jih začne s 4 ali 23, če se cifre ne smejo ponavljati?
d) Koliko se jih začne z 1 ali konča z 2, če se cifre lahko ponavljajo?
3) Koliko različnih števil lahko sestaviš, če uporabiš vsako od cifer 1,1,2,2,2,6,7,8 natanko enkrat?
4) Koliko različnih 7 mestnih števil lahko sestavimo z vsemi ciframi nabora 1, 1, 2, 2, 2, 6 in 7 ?
5) Koliko trimestnih števil lahko zapišemo s ciframi 1, 3, 5, 6, 8, 9,
a) če se cifre ne smejo ponoviti,
b) če se cifre lahko ponavljajo ?
6)
Imamo
cifre 
.
a) Na slepo izberemo eno cifro. Kolikšna je verjetnost, da je soda?
b) Vse cifre postavimo v vrsto. Kolikšna je verjetnost, da dobimo število 13542 ?
c) Na slepo izberemo dve cifri in ju seštejemo. Kolikšna je verjetnost, da dobimo vsoto 6 ?
7) Iz cifer 2,3,5,7,8,9 sestavljamo štirimestna števila. Koliko je takih števil,
a) če ne dovolimo ponavljanja cifer,
b) če lahko vsako cifro uporabimo večkrat?
8) S ciframi 1,3,4,5,6,8,9 sestavljaš števila.
a) Koliko je vseh štirimestnih števil, če se cifre lahko ponavljajo,
b) koliko je petmestnih sodih števil, če se cifre ne smejo ponavljati,
c) koliko števil med 700 in 5000 lahko sestaviš, če se cifre lahko ponavljajo?
9) S ciframi 2, 3, 4, 6 sestavljamo trimestna števila. Cifre se lahko poljubno ponavljajo. Kolikšna je verjetnost, da v naključno sestavljenem številu ne nastopa nobena cifra več kot enkrat?
10) S ciframi 1, 2, 3, 4, 45, 6, 7 sestavljamo števila.
a) Koliko je 4–mestnih števil, če se cifre ne smejo ponavljati?
b) koliko je števil med 500 in 6000, če se cifre lahko ponavljajo?
11) S ciframi 1,3,4,5,6,8,9 sestavljaš štirimestna števila.
a) Koliko je vseh takih števil, če se cifre lahko ponavljajo?
b) Koliko števil je sodih, če se cifre ne smejo ponavljati?
c) Na slepo izberi eno število iz primera b). Kolikšna je verjetnost, da je 8 edina soda cifra, ki jo število vsebuje?
12) S ciframi 2, 3, 5, 7, 9 sestavljamo štirimestna števila (cifre se lahko ponavljajo). kolikšna je verjetnost, da je na slepo sestavljeno število sodo in so vse cifre v njem različne?
Črke
1) Koliko različnih besed je mogoče sestaviti iz črk besede EKONOMISTKA, če se morajo besede začeti s T?
2) Koliko različnih “besed” lahko sestaviš, če uporabiš vse črke besede ŠTEVILO natanko enkrat in
a) ni dodatnih zahtev,
b) naj se beseda začne s samoglasnikom,
c) se beseda ne sme končati s skupino “VT”.
3) Na 6 listkih so napisane črke A, C, I, J, O, Ž.
a) Koliko različnih besed dobiš, če jih postavljaš v vrsto ?
b) Koliko teh besed se začne z dvema soglasnikoma ?
c) Na slepo postaviš v vrsto 4 črke. Kolikšna je verjetnost, da je nastala beseda ŽICA ?
4) Na voljo imaš vse črke besede MATEMATIKA.
a) Koliko različnih besed lahko sestaviš?
b) Koliko besed se začne s črko E ?
c) Kolikšna je verjetnost, da sestaviš ravno besedo AKITAMETAM ?
5) Na listkih imamo zapisane črke A, B, Č, E, R, O, Š, I in Ž. Samoglasniki so zapisani na zelenih listkih, šumniki na modrih in ostale črke na belih. Na koliko načinov lahko postavimo črke v vrsto,
a) če ni dodatnih omejitev,
b) če morajo samoglasniki stati na sodih mestih v besedi,
c) če morajo biti listki istih barv skupaj?
6) Na 6 listkih so napisane črke A, C, I, J, O, Ž.
a) Koliko različnih besed dobiš, če jih postavljaš v vrsto ?
b) Koliko teh besed se začne z dvema soglasnikoma ?
c) Na slepo postaviš v vrsto 4 črke. Kolikšna je verjetnost, da je nastala beseda ŽICA ?
7) Na voljo imaš vse črke iz besede FILOZOFIJA. Koliko različnih besed lahko sestaviš,
a) če je razporeditev poljubna,
b) če je zadnja črka obvezno A,
c) če morajo samoglasniki stati na sodih mestih v besedi ?
8) Dane so ploščice s črkami besede DEŽNIK.
a) Na slepo izberemo eno ploščico. Kolikšna je verjetnost, da bo izbrana črka Ž ?
b) Vse ploščice postavimo v vrsto. Kolikšna je verjetnost, da bo nastala ravno beseda DEŽNIK
c) Na slepo v vrsto postavimo tri ploščice. Kolikšna je verjetnost, da do nastala beseda DEŽ ?
9) Na voljo imaš vse črke iz besede EKONOMISTKA. Koliko različnih besed lahko sestaviš,
a) če je razporeditev poljubna,
b) če je prva črka obvezno T ?
c) Kolikšna je verjetnost, da na slepo sestavim ravno besedo EKONOMISTKA ?
10) Na voljo imaš vse črke besede POMLAD.
a) Na slepo izbereš eno črko. Kolikšna je verjetnost, da je ta črka samoglasnik?
b) Vse črke postavi na slepo v vrsto. Kolikšna je verjetnost, da nastane ravno beseda POMLAD?
c) Izberi 4 črke. Kolikšna je verjetnost, da si izbral črke M, A, L in O pri čemer vrstni red ni pomemben?
11) Koliko različnih besed lahko sestaviš iz vseh črk besede KONTROLKA,
a) če ni dodatnih omejitev,
b) če se beseda ne sme končati s črko T?
c) Kolikšna je verjetnost, da se beseda, ki jo dobiš, če črke slučajno postaviš v vrsto, začne s skupino KAR?
12) Koliko različnih “besed” lahko sestaviš, če porabiš vse črke iz besede POLNOLETNOST in
a) ni dodatnih omejitev,
b) se mora beseda začeti s črko S,
c) morajo biti vsi soglasniki na začetku besede?
13) Koliko različnih besed lahko sestaviš iz vseh črk besede KONTROLORKA,
a) če ni dodatnih omejitev,
b) če se beseda ne sme končati s črko T?
c) Koliko besed se začne s skupino LAT?
14) Koliko različnih besed lahko sestaviš iz črk RAZLIČNOST? Koliko se jih začne in konča s soglasnikom?
Rožice in drevesa
1) Na voljo imam 10 različnih rdečih cvetic in 15 različnih belih cvetic. Na koliko načinov lahko naredim šopek s 5 cveticami,
a) če so v šopku poljubne rože,
b) če morajo biti 3 rože rdeče in 2 beli,
c) če morata biti vsaj dve roži vsake barve?
2) V ravno vrsto želimo posaditi 5 tulipanov, 4 gerbere in 4 hiacinte. Vse rože so različnih barv. Na koliko načinov lahko to storimo,
a) če je razporeditev poljubna,
b) če morajo biti istovrstne skupaj ?
c) če moramo posaditi najprej tulipane, nato gerbere in na konec hiacinte ?
3) Na razpolago imamo 8 različnih rdečih cvetic in 10 različnih belih cvetic. Na koliko načinov lahko sestavimo šopek s 5 različnimi cveticami,
a) če je izbira poljubna,
b) če morajo biti v šopku 3 cvetice rdeče in 2 beli,
c) če morata biti vsaj 2 cvetici vsake barve ?
4) Vrtnar mora posaditi v vrsto 3 rdeče, 4 rumene, 3 bele in 5 oranžnih vrtnic. Vrtnic enake barve med sabo ne razlikuje. Na koliko načinov jih lahko posadi,
a) če morajo biti vrtnice istih barv skupaj,
b) če je razporeditev povsem poljubna?
Knjige, revije, kultura
1) Na koliko načinov lahko razporedimo v vrsto 5 križankarskih revij, 4 revije z nasveti za dom, 3 revije s TV sporedi in 3 revije, ki prinašajo “novice” iz življenja slavnih ljudi, (revije, ki so iste vrste, niso med sabo enake)
a) če ni dodatnih omejitev,
b) če morajo istovrstne revije ležati skupaj,
c) če morajo samo revije s TV sporedi ležati skupaj, ostale pa so lahko med sabo pomešane?
2) Štirje prijatelji Anže, Bine, Cene in Dore so se dogovorili, da bodo v soboto zvečer povabili v disko Fani, Gino, Irmo in Jožico.
a) Na koliko različnih načinov se lahko dogovorijo, katero bo kdo povabil?
b) Odpeljali so se v dveh avtomobilih. Na koliko načinov lahko določijo še tri sopotnike, ki se bodo peljali v Anžetovem starem fičku? (ni važno, na katerem sedežu bo kdo sedel)
c) Ko so prišli do diska, so se postavili v vrsto, da kupijo karte. Na koliko načinov se lahko vseh osem postavi v vrsto?
3) V galeriji pripravljajo razstavo. Eno ob drugo bodo na raven zid obesili 4 tihožitja, 3 portrete in 7 bolj ali manj abstraktnih slik. Na koliko načinov lahko to storijo,
a) če ni dodatnih omejitev,
b) če morajo istovrstne slike viseti skupaj,
c) če morajo samo portreti viseti skupaj?
4) Starši so dovolili trem bratom, da se vsak od njih naroči na eno revijo. Izbirajo lahko med 5 različnimi revijami. Na koliko načinov si lahko razdelijo naročnine,
a) če se vsak naroči na drugo revijo,
b) če se lahko dva ali tudi vsi trije naročijo na isto revijo?
Šport
1) Na nogometnem turnirju sodeluje 12 ekip. Vsaka ekipa odigra z vsako po eno tekmo. Koliko je vseh odigranih tekem?
2) V teku na 3000 m z ovirami sodeluje 14 tekmovalcev. na koliko na činov lahko zasedejo prva tri mesta? (delitev mest ni mogoča)
3) V teku na 3000 m z ovirami nastopa 15 tekmovalcev.
a) Na koliko načinov lahko zasedejo prva tri mesta ?
b) Kolikšna je verjetnost, da pred tekmo pravilno napovem, kateri trije bodo dobili medalje, vendar ne nujno v pravem vrstnem redu ?
4) Hokejski trener ima na voljo 15 igralcev. Koliko različnih napadalnih trojk lahko sestavi?
Šolarji in ostali ljudje
1) V skupini 10 otrok se 4 pišejo Novak, 3 Kralj in 3 Pavlin. Na koliko načinov se lahko postavijo v vrsto,
a) če je razporeditev poljubna,
b) če morajo otroci z enakim priimkom stati skupaj,
c) če morajo vsi “Kralji” stati skupaj?
2) V komisiji je 7 Nemcev in 8 Angležev. Na koliko načinov lahko izvolijo predsednika, podpredsednika in zapisnikarja v komisiji,
a) če ni dodatnih omejitev,
b) če morata imeti podpredsednik in zapisnikar drugačno narodnost kot predsednik.
3) Na neki zabavi so si 153-krat izmenjali najboljše želje ob novem letu. Koliko ljudi je bilo na zabavi, če je vsak voščil vsakemu?
4) V razredu je 27 učencev, od tega 6 fantov. Na koliko načinov lahko sestavijo tričlansko delegacijo, v kateri mora biti vsaj en fant?
5) Izmed 10 učiteljev in 20 dijakov je treba izbrati 3 člansko delegacijo. Na koliko načinov lahko to storimo,
a) če ni dodatnih omejitev,
b) če morata biti v delegaciji 2 učenca in en učitelj?
6) V vrsto želimo postaviti 3 sestre iz ene družine, 2 brata iz druge in 4 brate iz tretje. Na koliko načinov lahko to storimo,
a) če je razvrstitev poljubna,
b) če morajo sestre stati druga za drugo,
c) če sta brata iz druge družine dvojčka in ju ne ločimo?
7) V razredu je 15 učencev, ki jim bo učitelj postavil 4 vprašanja. Na koliko načinov lahko to stori, (pomembno je tudi, katero vprašanje dobi kakšen dijak)
a) če noben učenec ne more dobiti več kot enega vprašanja,
b) če je lahko vsak učenec vprašan večkrat?
8) Učenec ima na mizi 5 učbenikov in 4 leposlovne knjige. Na koliko načinov lahko izbere 4 knjige,
a) če so to poljubne knjige,
b) če mora izbrati 2 učbenika in 2 leposlovni knjigi,
c) če ne sme izbrati samo leposlovnih knjig?
9) Pri "malo drugačni" maturi lahko dijaki izberejo tri predmete poljubno. V nekem razredu, kjer je 30 dijakov, se jih je 14 odločilo za psihologijo, 12 za zgodovino in 12 za geografijo; 5 dijakov je izbralo psihologijo in zgodovino, 4psihologijo in geografijo, 7 zgodovino in geografijo; za vse te 3 predmete so se odločili 3 dijaki.
a) Koliko dijakov ni izbralo nobenega od teh treh predmetov,
b) koliko jih je izbralo samo zgodovino,
c) koliko jih je izbralo psihologijo in geografijo, vendar ne zgodovine?
10) V družbi je 6 žensk in 7 moških. Radi bi sestavili tričlansko delegacijo, ki bo preučila načrte za počitnice. Na koliko načinov lahko sestavijo to delegacijo,
a) če ni dodatnih omejitev,
b) če mora biti v delegaciji vsaj ena ženska,
c) če mora biti v delegaciji en določen moški?
Kroglice in zastavice
1) V posodi je 6 zelenih kroglic označenih z lihimi števili od 1 do 11 in 4 rdeče kroglice, označene s sodimi števili od 2 do 8.
a) Na koliko različnih načinov lahko izvlečeš hkrati 4 kroglice ?
b) Na koliko načinov lahko izvlečeš hkrati 4 kroglice, če ne smejo biti vse iste barve ?
c) Kolikšna je verjetnost, da hkrati izvlečeš vse tri kroglice, katerih oznake so deljive s 3 ?
d) Kolikšna je verjetnost, da izvlečeš najprej kroglico 6, nato zeleno kroglico in na koncu rdečo kroglico, če kroglic ne vračaš v posodo ?
2) Koliko različnih nizov s 4 ali 5 biseri lahko sestavimo, če imamo na voljo bisere v 10 različnih barvah in
a) lahko v nizu nastopa vsaka barva večkrat,
b) lahko vsako barvo uporabimo največ enkrat?
3) V posodi je 6 zelenih kroglic označenih z lihimi števili od 1 do 11 in 4 rdeče kroglice, označene s sodimi števili od 2 do 8.
a) Na koliko različnih načinov lahko izvlečeš hkrati 4 kroglice ?
b) Na koliko načinov lahko izvlečeš hkrati 4 kroglice, če ne smejo biti vse iste barve ?
c) Kolikšna je verjetnost, da hkrati izvlečeš vse tri kroglice, katerih oznake so deljive s 3 ?
d) Kolikšna je verjetnost, da izvlečeš najprej kroglico 6, nato zeleno kroglico in na koncu rdečo kroglico, če kroglic ne vračaš v posodo ?
4) Na voljo imamo bele, črne, rdeče, zelene in modre zastavice. Z njimi pošiljamo signale tako, da jih postavljamo v vrsto. Koliko različnih signalov lahko pošljemo,
a) če lahko postavimo v vrsto tri ali štiri raznobarvne zastavice,
b) če v vrsto postavimo tri ali štiri poljubne zastavice,
c) če postavimo v vrsto štiri zastavice tako, da dve istobarvni zastavici nista nikoli ena za drugo?
Ostala šara
1) Slaščičar prodaja 9 vrst keksov. Na koliko različnih načinov lahko pripravi zavitke s štirimi ali petimi keksi, če morajo biti keksi v zavitku različni med seboj?
2) Tovarna izdeluje sadne bonbone 4 različnih okusov. Na koliko različnih načinov lahko pakirajo zavitke po 15 bonbonov?
3) Nekdo ima v garderobi 4 pare čevljev, 2 obleki in 3 različna pokrivala. Na koliko načinov se lahko s tem obuje, obleče in pokrije ?
4) Iz kraja A v kraj B in nazaj vozi 5 avtobusov, iz kraja B kraj C in nazaj pa 3. Na koliko različnih načinov se lahko pripeljemo iz A v C in nazaj, če
a) smemo za povratek izbrati tudi tiste avtobuse, s katerimi smo se že peljali,
b) se ne smemo vračati z istimi avtobusi?
5) Nekdo ima v garderobi 6 parov čevljev, 3 obleke in 5 različnih pokrival. Na koliko načinov se lahko s tem obleče, obuje in pokrije? Na koliko načinov se lahko opravi, če pokrivalo ni nujen sestavni del garderobe?
6) V ravnini leži nekaj premic. Koliko je teh premic, če lahko skoznje potegnemo 78 premic, pri tem pa nobena premica ne poteka skozi 3 točke hkrati (ampak seveda skozi 2)?
Binomski izrek
1)
Podan
je binom 
.
a) Izračunaj tretji člen v razvoju tega binoma.
b)
Zapiši
tisti člen v razvoju, ki vsebuje 
.
2)
Izračunaj 
.
3)
Podan je binom 
a) Izračunaj deseti člen v razvoju tega binoma.
b)
Zapiši
tisti člen v razvoju, ki vsebuje 
.
4)
Zapiši sedmi člen v razvoju binoma 
v vrsto
5)
Izračunaj
6)
Podan
je binom 
a) Izračunaj deseti člen v razvoju tega binoma.
b) Zapiši tisti člen v razvoju, ki vsebuje x5.
7)
Zapiši
peti člen v razvoju binoma v vrsto !
8)
Izračunaj 
z razvojem po
binomskem izreku.
9)
Izračunaj
tako, da razviješ po binomskem izreku 
10)
Razvij
po binomskem izreku: 
11)
Izračunaj
z razvojem po
binomskem izreku.
12)
Podaj je
izraz 
. Zapiši in izračunaj vsoto 3., 4., in 5. člena v razvoju
tega binoma.
13)
Izračunaj
in zapiši tisti člen v razvoju binoma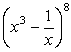 
, ki ne vsebuje spremenljivke x.
Enačbe s P in V
1)
Reši
enačbo 
2)
Okrajšaj
ulomek 
brez uporabe
kalkulatorja.
3)
Reši
enačbo: 
4)
Reši enačbo: 
Načelo vključitev in
izključitev
1) V nekem športnem društvu trenira 43 ljudi nogomet, 42 košarko in 41 atletiko; 21 članov se ukvarja z nogometom in atletiko, 15 z nogometom in košarko, 18 z atletiko in košarko; 8 vsestranskih športnikov se ukvarja z vsemi tremi športi.
a) Koliko je članov kluba?
b) Koliko jih trenira natanko 2 športa?
c) Koliko članov se ukvarja s košarko in atletiko ne pa tudi z nogometom?
2) Anketa, ki so jo izvedli med 100 ljudmi, je pokazala, da jih 60 hodi v kino, 55 na razstave in 75 v gledališče; 30 jih zahaja v kino in na razstave, 40 na razstave in v gledališče ter 45 v kino in gledališče; 20 ljudi se udeležuje vseh treh vrst prireditev.
a) Koliko ljudi ne hodi nikamor?
b) Koliko jih hodi samo v kino?
c) Koliko od ljudi, ki se udeležujejo prireditev, ne hodi na razstave?
3) Skupina ljudi obiskuje jezikovne tečaje. 36 ljudi se udeležuje tečaja iz angleškega jezika, 62 francoskega in 53 nemškega; 22 jih obiskuje francoščino in angleščino, 19 angleščino in nemščino, 24 francoščino in nemščino; na vseh treh tečajih se srečuje 14 ljudi.
a) Koliko je vseh obiskovalcev teh treh tečajev?
b) Koliko se jih uči samo enega jezika?
c) Koliko jih hodi k francoščini in nemščini, ne pa k angleščini?
4) Med naključno izbranimi obiskovalci knjižnice so nekega dopoldneva naredili anketo, ki je pokazala, da jih 29 bere kriminalke, 30 ljubezenske zgodbe in 19 znanstveno literaturo; 12 se jih navdušuje za kriminalke in ljubezenske zgodbe, 13 za kriminalke in znanstveno literaturo, 11 za znanstveno literaturo in ljubezenske zgodbe; 8 jih nosi domov knjige vseh treh vrst. Izmed anketirancev na slepo izberemo enega bralca. Izračunaj koliko od teh ljudi:
a) bere samo knjige ene vrste,
b) bere vse tri zvrsti literature,
c) bere kriminalke in ljubezenske zgodbe, ne bere pa znanstvene literature,
d) bere kriminalke in znanstveno literaturo.
5) Med 100 občani jih 60 hodi v kino, 55 na razstave in 75 v gledališče; 30 jih zahaja v kino in na razstave, 40 na razstave in v gledališče ter 45 v kino in gledališče; 20 ljudi se udeležuje vseh treh vrst prireditev.
a) Koliko ljudi ne hodi nikamor ?
b) Koliko jih hodi samo v kino ?
c) Na slepo izberemo 2 človeka. Kolika je verjetnost, da hodi v kino in gledališče, ne pa na razstave ?
6) V neki vasi, kjer je 200 hiš, berejo ljudje Delo, Republiko in Slovenca. Delo berejo v 100 hišah, Republiko v 95 in Slovenca v 90; Delo in Slovenca berejo v 40 hišah, Delo in Republiko v 35, Republiko in Slovenca v 55; vse tri časopise berejo v 25 hišah.
a) v kolikih hišah ne berejo nobenega od teh treh časopisov,
b) v koliko hišah berejo vsaj dva časopisa,
c) v koliko hišah berejo samo Delo?
7) Med naključno izbranimi 200 sprehajalci so naredili anketo o spremljanju TV programa. 66 ljudi je reklo, da spremljajo informativne oddaje, 95 jih gleda zabavne oddaje, 73 pa šport; informacije in zabavo išče 37 ljudi, informacije in šport 27 ter zabavo in športne prenose 29 ljudi; vse tri vrste oddaj spremlja 16 ljudi.
a) Koliko ljudi (od vprašanih) ne gleda navedenih oddaj po televiziji?
b) Koliko jih gleda le eno vrsto oddaj?
c)
Na
slepo izberemo enega anketiranca. Izračunaj verjetnost, da gleda športne
prenose, če vemo, da ne mara informativnih oddaj.
nazaj