Naloge za pripravo na maturo
- Dani sta množici A = {50n;
n ∈
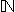 }
in B = {4n - 4;
n ∈
}
in B = {4n - 4;
n ∈ 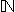 }.
Zapiši (s formulo) množico
C = A ∩ B.
}.
Zapiši (s formulo) množico
C = A ∩ B.
- Razcepi (preoblikuj v obliko produkta) naslednji izraz:
(2x + y + 1)2 −
(x − 2y + 1)2
-
Atlas sveta se je podražil za 20%, pozneje pa še za 15%. Zdaj stane 121,44 evrov. Izračunaj, koliko je stal
v začetku (pred prvo podražitvijo).
- Dani sta točki A(5,− 3) in B (3,2). Zapiši (v implicitni obliki) enačbo premice, ki
poteka skozi točko B in je pravokotna na daljico AB.
- Reši sistem enačb:
x − 2y = 7,
y + z = 2,
2x − z = 2
- Določi u tako, da bo imela dana enačba točno eno
rešitev. To rešitev tudi izračunaj!
3u x2 − (6u − 6)x + (3u − 5) = 0
- Reši enačbo:
3x − 2 − 3 · 4x − 3 =
3 · 4x − 2 – 3x − 1 + 4x − 3
-
Poenostavi izraz:
log (6x + 6) − log 3 − (log (x + 1) − log x)
Rezultat zapiši kot logaritem enočlenika.
- Konstruiraj pravokotnik s stranico a = 4 cm, če veš, da meri
kot med diagonalama 60°.
- Trikotnik je podan s podatki vc = 6 cm,
α = 35°, β = 65°. Izračunaj, koliko meri
tc. Rezultat zaokroži na štiri mesta.
- Poševna piramida ima za osnovno ploskev (vodoraven) kvadrat
ABCD z diagonalo d = 5 cm. Vrh te piramide leži točno 5 cm nad
ogliščem B. Izračunaj površino in prostornino te piramide.
- Pokaži, da je vrednost danega izraza točno enaka
sin 20°:
- Nariši graf funkcije: f (x) = 3 sin 2x + 1
- Reši enačbo: sin2x + sin 2x
− 3 cos2x = 0
- Izračunaj kot med premicama
3 + x = 0 in 2x + y = 7. Rezultat zapiši v stopinjah in minutah.
- Poišči vse ničle polinoma:
p(x) = x4 + x3 −
5x2 − 3x + 6
- Nariši graf funkcije:
- Reši neenačbo:
x3 − x < 3x
- Dana je premica p: y = 6 − 2x.
Zapiši enačbo krožnice, ki ima središče v presečišču premice p z abscisno
osjo in poteka skozi točko A(− 4,1).
- Na koliko načinov se lahko razporedi na (dolgi ravni) klopi 10 ljudi,
če želita sedeti Andraž in Binca skupaj, drugim pa je vseeno, kako sedijo?
- V posodi je 5 zelenih, 3 bele in 4 črne kroglice. Iz posode na slepo
potegnemo tri kroglice (naenkrat). Izračunaj verjetnosti dogodkov:
A: da je vsaj ena od kroglic bela,
B: da ni nobena od kroglic zelena.
- Določi realno število m tako, da bodo števila
m + 5, m,
 tvorila aritmetično zaporedje.
tvorila aritmetično zaporedje.
- Izračunaj kot med premico
 in
krivuljo
in
krivuljo  v točki T (3,0).
v točki T (3,0).
- Izračunaj stacionarne točke in nariši graf funkcije
- Izračunaj ploščino lika, ki ga oklepata abscisna os
in graf funkcije
f (x) = x3 + 2x2.
Rešitve
-
C = {100n;
n ∈
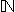 }
}
- (x + 3y)(3x − y + 2)
-
Prej je stal 88 evrov.
-
2x − 5y + 4 = 0
-
x = 3, y = − 2, z = 4
-
Dve možnosti:
(a) iz D = 0 dobimo u = 3, x = 2/3,
(b) iz a = 0 dobimo u = 0, x = 5/6
-
x = 2
- log 2x
- /
-
tc = 6,678 cm
-
V = 20,83 cm3, P = 51,83 cm2
- /
- /
-
x1 = π /4 + kπ,
x2 = − arc tg 3 + kπ
(k ∈ 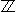 )
)
-
26°34'
-
1, − 2, √3, − √3
- /
- x < − 2 ali 0 < x < 2
-
(x − 3)2 + y2 = 50
-
725 760
-
P (A) = 0,618; P (B) = 0,159
-
m = 8 (opozorilo: m = 3 ni rešitev!)
-
90°
-
Maksimum M (− 2,− 1/4)
-
S = 4/3
Opravičujem se za morebitne napake pri tipkanju! Za odkrito napako
ne ponujam
zlatnika.
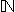 }
in B = {4n - 4;
n ∈
}
in B = {4n - 4;
n ∈ 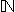 }.
Zapiši (s formulo) množico
C = A ∩ B.
}.
Zapiši (s formulo) množico
C = A ∩ B.
 tvorila aritmetično zaporedje.
tvorila aritmetično zaporedje.
 in
krivuljo
in
krivuljo  v točki T (3,0).
v točki T (3,0).
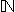 }
}
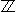 )
)