
All the objects considered so far have been "fixed stars", which keep the same values of Right Ascension and declination. But bodies within the Solar System change their celestial positions.
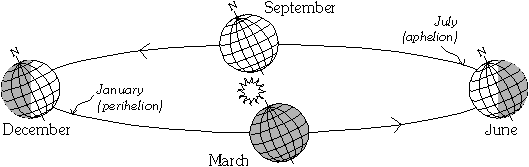
The most important one to consider is the Sun. The Sun's declination can be found by measuring its altitude when it's on the meridian (at midday). The Sun's Right Ascension can be found by measuring the Local Sidereal Time of meridian transit. We find that the Sun's RA increases by approximately 4 minutes a day, and its declination varies between +23°26' and -23°26'. This path apparently followed by Sun is called the ecliptic.

The reason is the tilt of the Earth's axis to its orbital plane. The angle of tilt is +23°26', which is called the obliquity of the ecliptic (symbol epsilon).
Any two great circles intersect at two nodes. The
node where the Sun crosses the equator from south to north (the
ascending node) is called the vernal (or spring) equinox.
This is the point from which R.A. is measured, so here RA = 0h.
At RA = 12h, the descending node is called the autumnal equinox.
At both these points, the Sun is on the equator, and spends 12 hours above
horizon and 12 hours below. ("Equinox" means "equal night",
night equal to day.)
The most northerly point of the ecliptic is called (in
the northern hemisphere) the Summer Solstice (RA = 6h), and the
most southerly point is the Winter Solstice (RA = 18h).
At the northern Summer Solstice, the northern hemisphere of Earth is tipped
towards Sun, giving longer hours of daylight and warmer weather (despite
the fact that Earth's slightly elliptical orbit takes it furthest from
the Sun in July!)
Thus the Sun's motion is simple when referred to the ecliptic; also the Moon and the planets move near to the ecliptic. So the ecliptic system is sometimes more useful than the equatorial system for solar-system objects.

In the ecliptic system of coordinates, the fundamental great circle is the ecliptic. The zero-point is still the vernal equinox. Take K as the northern pole of the ecliptic, K' as the southern one.
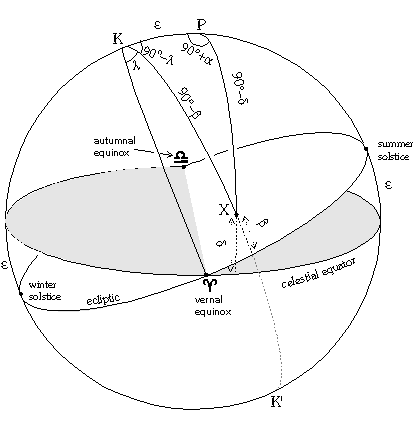
To fix the ecliptic coordinates of an object X on the celestial sphere, draw the great circle from K to K' through X.
The ecliptic (or celestial) latitude of X (symbol beta) is the angular distance from the ecliptic to X, measured from -90° at K' to +90° at K. Any point on the ecliptic has ecliptic latitude 0°.
The ecliptic (or celestial) longitude of X (symbol lambda) is the angular distance along the ecliptic from the vernal equinox to the great circle through X. It is measured eastwards (like R.A.), but in degrees, 0°-360°.
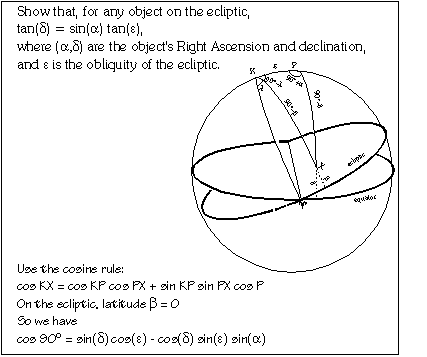
To convert between ecliptic and equatorial coordinates, use the spherical triangle KPX.
Return to index.